例1、电阻为R的导线矩形线框abcd的边长ab=l，bc=h，质量为m，自某一高度自由下落，通过一匀强磁场，磁场方向垂直纸面向里，磁场区域的宽度为h．若线框恰好以恒定速度通过磁场，线框中产生的焦耳热量为_______(不计空气阻力)．

解析一：

　　线框匀速通过磁场区域的过程中，沿竖直方向的位移为2h．在这过程中线框的动能不变，重力做功2mgh，重力势能减少2mgh，根据能量转化与守恒定律．减小的机械能全部通过电磁感应转化为内能，所以产生的焦耳热为2mgh．

解析二：

　　设线框通过磁场的恒定速度为v，则通过磁场所花时间为

　　

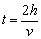
　　线框通过磁场时，感应电动势E=Blv，感应电流I=Blv/R，产生的焦耳热为

　　

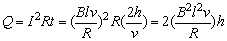
　　线框匀速通过磁场，所受合力为零，即BIl=mg，可得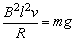，代入上式得

　　Q=2mgh

答案：2mgh

2、（上海）如图所示，两条互相平行的光滑金属导轨位于水平面内，距离为l=0.2m，在导轨的一端接有阻值为R=0.5Ω的电阻，在x≥0处有一与水平面垂直的均匀磁场，磁感应强度B=0.5T．一质量为m=0.1 kg的金属直杆垂直放置在导轨上，并以v0=2 m/s的初速度进入磁场，在安培力和一垂直于杆的水平外力F的共同作用下做匀变速直线运动，加速度大小为a=2m/s2，方向与初速度方向相反．设导轨和金属杆的电阻都可以忽略，且接触良好．求

(1)电流为零时金属杆所处的位置；

(2)电流为最大值的一半时施加在金属杆上外力F的大小和方向；

(3)保持其他条件不变，而初速度v0取不同值，求开始时F的方向与初速度v0取值的关系．

解析：（1）感应电动势E=Blv，I=E/R，

∴I=0时，v=0，

∴x=v02/(2a)=1m．

（2）最大电流Im=Blv0/R，

I′=Im/2=Blv0/(2R)．

安培力

f=I′Bl=B2l2v0/(2R)=0.02N．

向右运动时F＋F安=ma，

F=ma－F安=0.18N，方向沿x轴负方向．

向左运动时F－F安=ma，

F=ma＋F安=0.22N，方向沿x轴负方向．

（3）开始时v=v0，F安=ImBl=B2l2v0/R．

F＋F安=ma，

F=ma－F安=ma－ B2l2v0/R．

∴当v0<maR/(B2l2)=10m/s时，F>0，方向沿x轴负方向．

当v0>maR/(B2l2)=10m/s时，F<0，方向沿x轴正方向．

3、（天津）如图所示，两根平行的金属导轨，固定在同一水平面上，磁感应强度B=0.50T的匀强磁场与导轨所在平面垂直，导轨的电阻很小，可忽略不计．导轨间的距离l=0.20 m．两根质量均为m=0.10 kg的平行金属杆甲、乙可在导轨上无摩擦地滑动，滑动过程中与导轨保持垂直，每根金属杆的电阻为R=0.50Ω．在t=0时刻，两杆都处于静止状态．现有一与导轨平行、大小与0.20 N的恒力F作用于金属杆甲上，使金属杆在导轨上滑动．经过t=5.0s，金属杆甲的加速度为a=1.37m/s2，问此时两金属杆的速度各为多少?

解析：

　　设任一时刻t两金属杆甲、乙之间的距离为x，速度分别为v1和v2，经过很短时间△t，杆甲移动距离v1△t，杆乙移动距离v2△t，回路面积改变

△S=[(x－v2△t)＋v1△t]－lx=(v1－v2)l△t

由法拉第电磁感应定律，回路中的感应电动势

回路中的电流

由牛顿第二定律，对杆甲有

F－BlI=ma

由于作用于杆甲和杆乙的安培力总是大小相等、方向相反，所以两杆的动量(t=0时为0)等于外力F的冲量，

Ft=mv1＋mv2

联立以上各式解得

代入数据得

v1=8.15m/s，v2=1.85m/s．

-END-