电容器与电容在高考中时常会出现一些定性分析的问题，而带电粒子在匀强电场中的运动则往往是高考重点考察内容，因为这一部分内容，常与力学的主干知识联系紧密，有的还与科学、社会中的问题密切相关。

例、为研究静电除尘，有人设计了一个盒状容器，容器侧面为绝缘透明的有机玻璃，它的上、下底面是面积A=0.04m2的金属板，间距L=0.05m，当连接到U=2500V的高压电源正负两极时，能在两极板间产生一个匀强电场，如图所示，现把一定量均匀分布的烟尘颗粒密闭在容器内，每立方米有烟尘颗粒1023个，假设这些颗粒都处于静止状态，每个颗粒带电量为q=＋1.0×10－17C，质量为m=2.0×10－15kg，不考虑烟尘颗粒之间的相互作用和空气阻力，并忽略烟尘颗粒所受重力。求合上电键S后：

（1）经过多少时间烟尘颗粒可以被全部吸附？

（2）除尘过程中电场对烟尘颗粒共做了多少功？

（3）经过多长时间容器中烟尘颗粒的总动能达到最大？

 

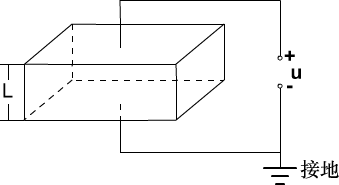
解析：

　　静电除尘是静电的重要应用之一，本题实际上是多个粒子在匀强电场中运动的问题。

　　（1）当最靠近上表面的烟尘颗粒被吸附到下板时，烟尘就被全部吸附。

　　　　 烟尘颗粒受到的电场力为.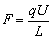

　　　　烟尘颗粒在电场中做匀加速直线运动，则：

　　　　

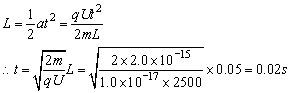
　　　　即经 0.02s被全部吸附.

　　（2）容器内的烟尘颗粒总数为NAL。

　　一个颗粒从上极板到下极板时，电场力的功为 qU，当全部烟尘颗粒都被吸附时，电场力所做的总功为：

　　　　

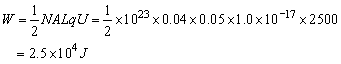
（3）设烟尘颗粒下落距离为x时，总动能为：

　　

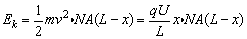
　　式中 NA（L－x）为烟尘颗粒下落x距离后的总颗粒数.

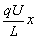　　是电场力对一个颗粒做的功.

　　当 x=L－x时上式左边有最大值，即x=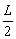时，Ek最大.

　　

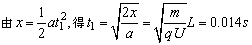
　　即经 t1=0.014s容器中烟尘颗粒的总动能最大.

-END-