|
一、一周内容概述
光电效应现象及其规律,光子说和爱因斯坦的光电效应的方程、光的波粒二象性是本章的重点和难点知识;理解光电效应的规律与经典的光的波动理论的矛盾,会用爱因斯坦的光子说解释光电效应的规律,并会运用爱因斯坦的光电效应方程进行有关的计算;知道光是一种概率波,理解光的波动性与粒子性的统一。
二、重、难点知识归纳及讲解
(一)、光电效应
1、光电效应的现象:在光的照射下物体发射电子的现象,叫做光电效应,发射出来的电子叫做光电子,产生的电流叫光电流。
2、光电效应的规律
①任何一种金属都有一个极限频率,入射光频率必须大于这个极限频率,才能产生光电效应,低于这个频率的光不能发生光电效应,能否发生光电效应,不取决于光强,只取决于频率。
②光电子最大初动能与入射光的强度无关,只随入射光频率的增大而增大。
③入射光照射到金属上时,光电子的发射几乎是瞬时的,一般不超过10-9s。
④当入射光的频率大于极限频率时,单位时间从金属表面逸出的光电子数目与入射光的强度成正比。
归纳:

3、光电效应与光的电磁理论的矛盾
矛盾之一:按光的波动理论,不论光的频率如何,只要照射时间足够长或光的强度足够大就可以产生光电效应,但实验结果表明:产生光电效应的条件却是入射光频率大于某一极限频率,且光电效应的最大初动能与入射光频率成线性关系,均与光强无关。根据能量的观点,电子要从物体中飞出,必须使之具有一定的能量,而这一能量只能来源于照射光,为什么实验表明发射电子的能量与照射光的光强无关,而与光的频率有关?这个问题曾使物理界大为困惑,使经典的光的波动理论面临挑战。
矛盾之二:光电效应产生的时间极短。
当一束很细的光照射到物体上时,它的能量将分布到大量的原子上,怎么可能在极短时间内把足够的能量集中到电子上而使之从物体中飞出。
(二)、光子说
1900年,德国物理学家普朗克在研究电磁波的辐射规律时发现:只有假设电磁波的能量不是连续的,是一份一份地进行,每一份能量为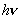 ,其中 ,其中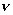 是辐射频率,h是普朗克恒量,这样才能使理论计算结果和实际相符。 是辐射频率,h是普朗克恒量,这样才能使理论计算结果和实际相符。
1905年爱因斯坦在普朗克建立的量子理论的基础上利用光子说成功地解释了光电效应现象及规律。
1、光子说:光是不连续的,而是一份一份的,每一份光叫光子,光子的能量E=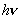 ,h=6.63×10-34J·s。 ,h=6.63×10-34J·s。
2、光子说对光效应规律的解释:
当光子照射到金属上时,它的能量被金属中的某个电子全部吸收,电子吸收能量后,动能增加。当它的动能足够大时,它能克服金属内部原子核对它的吸引而离开金属表面逃逸出来,成为光电子,光电子的发射时间很短,不需要能量的积累过程。
电子吸收光子的能量后,可能向各个方向运动,有的向金属内部运动,有的向外运动,由于路程不同,电子逃逸出来时损失的能量不同,因而它们离开金属表面的初动能不同。只有直接从金属表面飞出来的电子的初动能最大,这时光电子克服原子核的引力所做的功叫这种金属的逸出功W。
对于某一金属而言,逸出功W一定,故入射光的频率越大,光电子的最大初动能也越大;若入射光的频率比较低,使得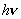 <W,就不能产生光电效应,若 <W,就不能产生光电效应,若 =W,这时光子的频率就是发生光电效应的极限频率。 =W,这时光子的频率就是发生光电效应的极限频率。
由于不同金属的逸出功不同,故它们的极限频率不同,照射光增强时,单位时间内入射的光子数增多,自然产生的光电子也越多。
(三)、光电效应方程
爱因斯坦认为,一个入射光子的能量只能被一个电子获得,这个电子能否从金属中逸出,取决于两个因素:一是电子获得了多少能量,即入射光子的能量有多大;二是金属对逸出电子的束缚导致电子逸出时消耗了多少能量。光电效应中,从金属表面逸出的电子消耗能量最少,因而有最大初动能。爱因斯坦提出:
Ek=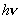 -W -W
其本质是能的转化和守恒的方程。
(四)、光学发展史
在上一章中,我们学习了光的干涉和衍射,由于干涉和衍射是波特有的现象,故知道光是一种波,并且知道光是一种电磁波。
但是,光电效应现象又无法用光的波动学说来解释,爱因斯坦提出“光子说”能圆满解释光电效应现象,光的粒子性又得到认同,直到二十世纪初,对于光的本性的认识才提升到一个更高层次,即光具有波粒二象性,对于光学发展史,列表如下:
学说 |
微粒说 |
波动说 |
电磁说 |
光子说 |
波粒二象性 |
代表人物 |
牛顿 |
惠更斯 |
麦克斯韦 |
爱因斯坦 |
公认 |
年代 |
17世纪 |
17世纪 |
19世纪中 |
20世纪初 |
20世纪初 |
(五)、光的波动性与粒子性的统一
1、大量光子产生的效果显示出波动性,个别光子产生的效果显示出粒子性。
2、光子和电子、质子等实物粒子一样,具有能量和动量。和其他物质相互作用时,粒子性起主导作用;在光的传播过程中,光子在空间各点出现的可能性的大小(概率),由波动性起主导作用,因此称光波为概率波。
3、光子的能量与其对应的频率成正比,而频率是波动性特征的物理量,因此E=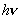 ,揭示了光的粒子性和波动性之间的密切联系。 ,揭示了光的粒子性和波动性之间的密切联系。
4、对不同频率的光,频率低、波长长的光,波动性特性显著;而频率高、波长短的光,粒子性特征显著。
综上所述,光的粒子性和波动性组成一个有机的统一体,相互间并不是独立存在。
(六)、从微观的角度理解光的波动性和粒子性
光既表现出波动性又表现出粒子性,很难用宏观世界的观念来认识,必须从微观的角度建立起光的行为图景,认识光的波粒二象性,需要明确的是:爱因斯坦光子说中的“粒子”和牛顿微粒中的“粒子”是两个完全不相同的概念;同样,麦克斯韦电磁说中的“波”与惠更斯波动说中的“波”也是不同理论领域中完全不同的概念,其本质区别在于微观世界的认识论与宏观世界的认识论的区别。
(七)、光波是概率波
在双缝干涉实验中,光子通过双缝后,对某一个光子而言,其运动是不可控制的,但对大量光子而言,它们落在光屏上的位置又有规律性,即某些区域光子落点多,另一些区域光子落点少,落点多的区域就是亮条纹,落点少的区域就是暗条纹,因此说光波是一种概率波。
三、典型例题解析
(一)、有关光电效应的问题主要是两个方面:一是关于光电效应的现象的判断,另一个就是运用光电效应方程进行简单的计算。解题的关键在于掌握光电效应规律,明确各概念之间的决定关系,有:

例1、用同一束单色光,在同一条件下先后照射锌片和银片,都能产生光电效应。在这两个过程中,对于下列四个量,一定相同的是_________,可能相同的是_______,一定不同的是________。
A.光子的能量 B.光电子的逸出功
C.光电子动能 D.光电子最大初动能
解答:
光子的能量由光频率决定,同一束单色光频率相同,因而光子能量相同。逸出功等于电子脱离原子核束缚需要做的最少的功,因此只由材料决定,锌片和银片的光电效应中,光电子的逸出功一定不相同。
由于 ,照射光子能量 ,照射光子能量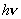 相同,逸出功W不同,则电子最大初动能也不同。由于光电子吸收光子后到达金属表面的路径不同,途中损失的能量也不同,因而脱离金属时的可能动能分布在零到最大初动能之间。所以,两个不同光电效应的光电子中,有时初动能是可能相等的 相同,逸出功W不同,则电子最大初动能也不同。由于光电子吸收光子后到达金属表面的路径不同,途中损失的能量也不同,因而脱离金属时的可能动能分布在零到最大初动能之间。所以,两个不同光电效应的光电子中,有时初动能是可能相等的
例2、由爱因斯坦光电效应方程可以画出光电子的最大初动能和入射光的频率的关系,如下图所示,以下说法正确的是( )
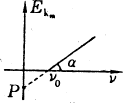
A.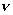 表示极限频率 表示极限频率
B.P的绝对值等于逸出功
C.直线的斜率表示普朗克常量h的大小
D.图线表明最大初动能与入射光频率成正比
解析:
由爱因斯坦光电效应方程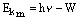 。可知当 。可知当 即为某金属的极限频率;当 即为某金属的极限频率;当 =0时, =0时,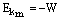 ,可见P的绝对值就是该金属对应的逸出功;而该直线的斜率 ,可见P的绝对值就是该金属对应的逸出功;而该直线的斜率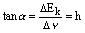 即为普朗克常量。故A、B、C正确。 即为普朗克常量。故A、B、C正确。
答案:ABC
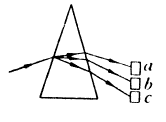
例3、一细束平行光经玻璃三棱镜折射后分解为互相分离的三束光,分别照射到相同的金属板a、b、c上,如图所示,已知金属板b有光电子放出,则可知( )
A.板a一定不放出光电子
B.板a一定放出光电子
C.板c一定不放出光电子
D.板c一定放出光电子
解析:
介质对不同频率的色光折射率不同,频率越高折射率越大,通过三棱镜后偏折得越厉害。由图可知,分别射向金属板a、b、c的三束光,频率越来越高。a、b、c是相同的金属板,发生光电效应的极限频率是相同的,b板有光电子放出,则c板有光电子放出,a板不一定有光电子放出,故选D。
答案:D
(二)、由于光子是光的能量的最小单位,因此在涉及发光能量问题的计算时,常常要计算光子总数。解此类题的基本思路是:根据题意建立模型,从能的转化与守恒的角度思考和求解问题,解题的关键在于审题和正确建立模型上。
例4、在单缝衍射实验中,中央亮纹的光强占从单缝射入的整个光强的95%以上,假设现在只让一个光子通过单缝,那么该光子( )
A.一定落在中央亮纹处
B.一定落在亮纹处
C.可能落在暗纹处
D.落在中央亮纹处的可能性最大
解析:
根据光的几率波的概念,对于一个光子通过单缝落在何处,是不可确定的,但概率最大的是落在中央亮纹处,可达95%以上。当然也可落在其他亮纹处,还可能落在暗纹处,不过,落在暗纹处的概率最小,故CD正确。
答案:CD
例5、太阳光垂直射到地面上时,1m2地面接受的太阳光的功率为1.4kW,其中可见光部分约点45%。
(1)假如认为可见光的波长约为0.55μm,日、地间距离R=1.5×1011m。普朗克常量h=6.6×10-34J·s,估算太阳每秒辐射出的可见光光子为多少?
(2)若已知地球的半径r为6.4×106m,估算地球接受太阳光的总功率。
解析:
(1)设地面上垂直阳光的1m2面积上每秒钟接收的可见光光子数为n,则有

设想一个以太阳为球心,以日、地距离为半径的大球面包围着太阳。大球面接受的光子数即等于太阳辐射的全部光子数。则所求可见光光子数。
N=n·4πR2=1.75×1021×4×3.14×(1.5×1011)2=4.9×1044(个)
(2)地球背着阳光的半个球面没有接收太阳光,地球向阳的半个球面面积也不都与太阳光垂直。接收太阳光辐射且与阳光垂直地有效面积是以地球半径为半径的圆平面的面积。则地球接收阳光的总功率:
P地=P·πr2=1.4×3.14×(6.4×106)2=1.8×1017(kW)
点评:
本题求解关键要明确两点:一是运用能量的转化和守恒原理,正确求得可见光光子数;二是正确建立模型,即以太阳为球心,日、地距离为半径的球面模型和以地球半径为半径的圆平面面积模型。
- 返回 -
|