| 电荷在电场中运动时,仅在电场力作用下运动时,要善于对运动过程进行分析,灵活运用牛顿定律和运动学公式式分析问题,从而解决问题。
例、如图所示,匀强电场E=2.0×103V/m,方向水平,电场中有两带电质点,它们的质量均为m=1.0×10-5kg,质点A带负电,质点B带正电,电量均为q=1.0×10-9C。开始时,两质点位于同一等势面上,A的初速度VAO=2.0m/s,B的初速度VBO=1.2m/s,均沿场强方向,在以后的运动过程中,若用△s表示任一时刻两质点间的水平距离,问当△s的数值在什么范围内,可判断哪个质点在前面(规定图中右方为前),当△s的数值在什么范围内不可判断谁前谁后?

解析:
带负电的质点 A所受电场力与场强方向相反,带正电的质点B所受的电场力与场强方向相同,因此,A作匀减速直线运动,B作匀加速直线运动,由于A的初速度VA0大于B的初速度VBO,故在开始阶段A的速度VA比B的速度VB大,A的位移SA比B的位移SB大,且A、B间的速度VA-VB是逐渐减小的,而A、B间的距离SA-SB逐渐增大,但过了一段时间后,B的速度超过A的速度,A、B间的距离SA-SB逐渐减小,故转折的条件是两者速度相等,即VA=VB,当VA=VB时,A、B间距SA-SB最大。
以 t1表示转折时刻,由运动学公式有:
VA0-at1=VBO+at1 (1)
A、B间的最大距离为:
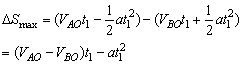 (2) (2)
由牛顿定律和题设条件,可得质点 A、B的加速度
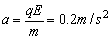 (3) (3)
由(1)、(2)、(3)式求得:
t1=2s,△Smax=0.8m
当发生转折后,即在 t>t1时,由于VB>VA,则A、B间的距离SA-SB逐渐减小,以t2表示A、B间距减小到零的时刻,则由运动学公式得:
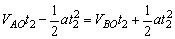
解得 t2=4s
当 t>t2时,由于VB>VA,故A、B间距将由O一直增大,有可能超过0.8m。
综上所述,当 A、B间的距离△S<0.8m时,A可能在前,B也可能在前,即单由A、B间的距离,无法判断A、B中哪个在前;当A、B间的距离△S>0.8m时,B一定在前,即单由A、B间的距离就可以判断B在前,A在后。
|