一、选择题
1、不等式 的解集是( ) 的解集是( )
A.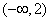 B. B.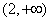
C. D. D. 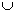 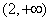
2、“a>0,b>0”是“ab>0”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3、若a>0,b>0,则不等式-b< <a等价于( ) <a等价于( )
A. <x<0或0<x< <x<0或0<x<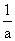 B.- B.-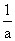 <x< <x<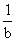
C.x<-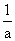 或x> 或x> D.x< D.x<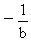 或x> 或x>
4、设f(x)= 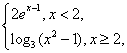 则不等式f(x)>2的解集为( ) 则不等式f(x)>2的解集为( )
A.(1,2)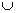 (3,+∞) B.( (3,+∞) B.( ,+∞) ,+∞)
C.(1,2)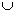 ( ( ,+∞) D.(1,2) ,+∞) D.(1,2)
5、若 ,则下列不等式成立的是( ) ,则下列不等式成立的是( )
A.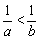 B. B.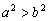
C.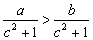 D. D.
6、已知不等式
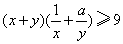 对任意正实数x,y恒成立,则正实数a的最小值为( ) 对任意正实数x,y恒成立,则正实数a的最小值为( )
A.2 B.4
C.6 D.8
7、已知函数f(x)=ax2+2ax+4(a>0),若x1<x2, x1+x2=0,则( )
A.f(x1)<f(x2) B.f(x1)=f(x2)
C.f(x1)>f(x2) D.f(x1)与f(x2)的大小不能确定
8、设实数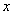 , ,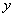 满足 满足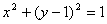 ,当x+y+c≥0时,c的取值范围是( ) ,当x+y+c≥0时,c的取值范围是( )
A.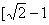 , ,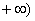 B. B. , ,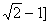
C. , ,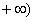 D. D.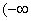 , ,
9、若关于x的不等式 ≤ ≤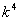 +4的解集是M,则对任意实常数k,总有( ) +4的解集是M,则对任意实常数k,总有( )
A.2∈M,0∈M B.2 M,0 M,0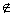 M M
C.2∈M,0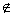 M D.2 M D.2 M,0∈M M,0∈M
10、若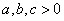 且 且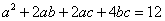 ,则 ,则 的最小值是( ) 的最小值是( )
A.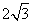 B.3 B.3
C.2 D.
[提示]
二、填空题
11、不等式 的解集是____________. 的解集是____________.
12、三个同学对问题“关于x的不等式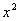 +25+| +25+|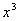 -5 -5 |≥ |≥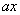 在[1,12]上恒成立,求实数a的取值范围”提出各自的解题思路. 在[1,12]上恒成立,求实数a的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量x的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于x的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即a的取值范围是________________.
13、某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和最小,则x=__________吨.
14、已知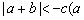 , , , ,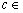 R)给出下列不等式: R)给出下列不等式:
① ;② ;② ; ③ ; ③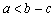 ;④ ;④ ;⑤ ;⑤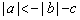 .其中一定成立的不等式是__________ (注:把成立的不等式的序号都填上). .其中一定成立的不等式是__________ (注:把成立的不等式的序号都填上).
15、已知直线l过点P(2,1),且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点,则三角形OAB面积的最小值为__________.
[答案]
三、解答题
16、若a>0,b>0,a3+b3=2.求证a+b≤2,ab≤1.
[答案]
17、对于在区间[m,n]上有意义的两个函数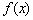 与 与 ,如果对任意的 ,如果对任意的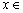 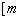 , ,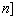 ,均有 ,均有 ≤1,则称 ≤1,则称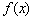 与 与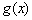 在区间 在区间 , ,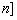 上是接近的,否则是非接近的.设 上是接近的,否则是非接近的.设 与 与 , ,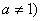 是区间 是区间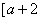 , ,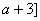 上的两个函数. 上的两个函数.
(1)求a的取值范围;
(2)讨论 与 与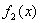 在区间 在区间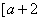 , ,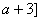 上是否是接近的. 上是否是接近的.
[答案]
18、己知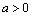 ,函数 ,函数 . .
(1)当 时,若对任意 时,若对任意 R都有 R都有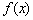 ≤1,证明: ≤1,证明: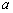 ≤ ≤ ; ;
(2)当 时,证明:对任意 时,证明:对任意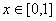 , , ≤1的充要条件是 ≤1的充要条件是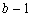 ≤ ≤ ≤ ≤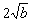 ; ;
[答案]
19、对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为: )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为 )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为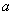 (1≤a≤3).设用x单位质量的水初次清洗后的清洁度是 (1≤a≤3).设用x单位质量的水初次清洗后的清洁度是 ( ( ),用y质量的水第二次清洗后的清洁度是 ),用y质量的水第二次清洗后的清洁度是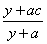 ,其中 ,其中 是该物体初次清洗后的清洁度. 是该物体初次清洗后的清洁度.
(Ⅰ)分别求出方案甲以及c=0.95时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙,当a为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论a取不同数值时对最少总用水量多少的影响.
[答案]
20、已知 为正整数, 为正整数,
(I)用数学归纳法证明:当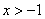 时, 时,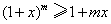 ; ;
(II)对于 ,已知 ,已知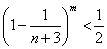 ,求证 ,求证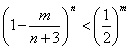 , ,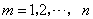 ; ;
(III)求出满足等式 的所有正整数 的所有正整数 . .
[答案]
|