1.已知函数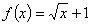 ,则
,则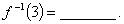
2.如果函数 ,那么
,那么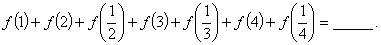
3.如果函数 的图象关于直线
的图象关于直线 对称,那么
对称,那么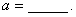
4.不等式 (
( )的解集为____________.
)的解集为____________.
5.以双曲线 的中心为焦点,且以该双曲线的左焦点为顶点的抛物线方程是____________.
的中心为焦点,且以该双曲线的左焦点为顶点的抛物线方程是____________.
6.设椭圆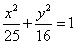 上一点
上一点 到左准线的距离为10,
到左准线的距离为10, 是该椭圆的左焦点,若点
是该椭圆的左焦点,若点 满足
满足 ,则
,则 =___________.
=___________.
7.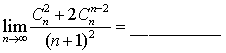 .
.
8.定义一种运算“ ”对于正整数满足以下运算性质:
”对于正整数满足以下运算性质:
(1) ;
;
(2)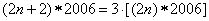 ,则
,则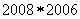 的值是___________.
的值是___________.
9.如果直线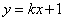 与圆
与圆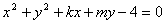 相交于
相交于 两点,且点
两点,且点 关于直线
关于直线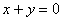 对称,则不等式组
对称,则不等式组 所表示的平面区域的面积为________.
所表示的平面区域的面积为________.
10.已知函数f(x)=Acos2(ωx+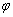 )+1(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(100)=____________.
)+1(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(100)=____________.
11.若函数 满足:对于任意
满足:对于任意 都有
都有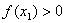 ,
,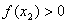 且
且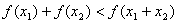 成立,则称函数
成立,则称函数 具有性质M.
具有性质M.
给出下列四个函数:①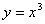 ,②
,②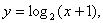 ③
③ ,④
,④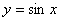 .
.
其中具有性质M的函数是___________.(注:把满足题意的所有函数的序号都填上)
12.如图,在杨辉三角中,斜线l上方,从1开始箭头所示的数组成一个锯齿数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于____________.
13. 已知f(x+y)=f(x)·f(y)对任意的实数x、y都成立,且f(1)=2,则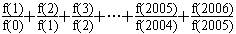 = __________.
= __________.
14.已知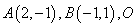 为坐标原点,动点
为坐标原点,动点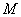 满足
满足 ,其中
,其中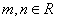 且
且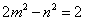 ,则
,则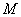 的轨迹方程为____________.
的轨迹方程为____________.
15.从装有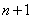 个球(其中
个球(其中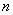 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出 个球
个球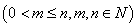 ,共有
,共有 种取法。在这
种取法。在这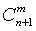 种取法中,可以分成两类:一类是取出的
种取法中,可以分成两类:一类是取出的 个球全部为白球,共有
个球全部为白球,共有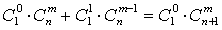 ,即有等式:
,即有等式: 成立.试根据上述思想化简下列式子:
成立.试根据上述思想化简下列式子:
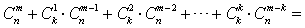 ____________.
____________. .
.
16.数列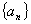 中,
中,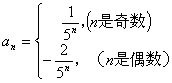 ,
, , 则
, 则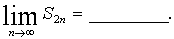
17.正三棱锥P-ABC的底面边长为1,E、F、G、H分别是PA、 AC、BC、PB的中点,四边形EFGH的面积为S,则S的取值范围是____________.
18.若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积是____________(只需写出一个可能的值).
19.椭圆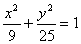 上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是__________.
上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是__________.
20.一只酒杯的轴截面是抛物线的一部分,它的函数解析式是 ,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.