一、选择题
1、若 ,则a的取值范围是( ) ,则a的取值范围是( )
A. B. B.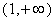
C. D. D.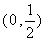
2、下列结论正确的是( )
A.当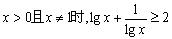
B.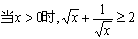
C. 的最小值为2 的最小值为2
D.当 无最大值 无最大值
3、在R上定义运算 : : .若不等式 .若不等式 对任意实数x成立,则( ) 对任意实数x成立,则( )
A. B. B.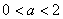
C. D. D.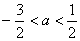
4、设a、b、c是互不相等的正数,则下列不等式中不恒成立的是( )
A. B. B.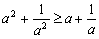
C. D. D.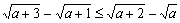
5、若动点( )在曲线 )在曲线 上变化,则 上变化,则 的最大值为( ) 的最大值为( )
A. B. B.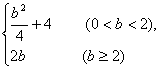
C. D.2b D.2b
6、已知向量 ≠ ≠ ,| ,| |=1,对任意t∈R,恒有| |=1,对任意t∈R,恒有| -t -t |≥| |≥| - -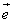 |,则( ) |,则( )
A. ⊥ ⊥ B. B. ⊥( ⊥( - - ) )
C. ⊥( ⊥( - - ) D.( ) D.( + + )⊥( )⊥( - - ) )
7、已知函数 在区间 在区间 上的最小值是 上的最小值是 ,则 ,则 的最小值等于( ) 的最小值等于( )
A. B. B.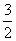
C.2 D.3
8、设 ,对于函数 ,对于函数 ,下列结论正确的是( ) ,下列结论正确的是( )
A.有最大值而无最小值
B.有最小值而无最大值
C.有最大值且有最小值
D.既无最大值又无最小值
9、在约束条件 下,当 下,当 时,目标函数 时,目标函数 的最大值的变化范围是( ) 的最大值的变化范围是( )
A. B. B.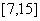
C. D. D.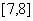
10、已知不等式 对任意正实数 对任意正实数 恒成立,则正实数 恒成立,则正实数 的最小值为( ) 的最小值为( )
A.2 B.4
C.6 D.8
[提示]
二、填空题
11、已知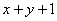  ,则 ,则 的最小值是__________. 的最小值是__________.
12、在△OAB中,O为坐标原点, ,则△OAB的面积达到最大值时, ,则△OAB的面积达到最大值时, __________. __________.
13、设实数x, y满足 __________. __________.
14、在 中,O为中线AM上一个动点,若AM=2,则 中,O为中线AM上一个动点,若AM=2,则 的最小值是__________. 的最小值是__________.
15、已知函数 在[0,1]上的最大值与最小值的和为a,则a的值为____________. 在[0,1]上的最大值与最小值的和为a,则a的值为____________.
[答案]
三、解答题
16、若函数 的最大值为 的最大值为 ,试确定常数a的值. ,试确定常数a的值.
[答案]
17、已知函数f(x)=x3+ax2+bx+c在x=- 与x=1时都取得极值. 与x=1时都取得极值.
(1)求a、b的值与函数f(x)的单调区间.
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
[答案]
18、已知函数 ,其中0<a<4. ,其中0<a<4.
(Ⅰ)将 的图像向右平移两个单位,得到函数 的图像向右平移两个单位,得到函数 ,求函数 ,求函数 的解析式; 的解析式;
(Ⅱ)函数 与函数 与函数 的图像关于直线 的图像关于直线 对称,求函数 对称,求函数 的解析式; 的解析式;
(Ⅲ)设 ,已知 ,已知 的最小值是 的最小值是 ,且 ,且 ,求实数 ,求实数 的取值范围. 的取值范围.
[答案]
19、已知中心在原点的双曲线C的右焦点为(2,0),右顶点为 . .
(1)求双曲线C的方程;
(2)若直线l: 与双曲线C恒有两个不同的交点A和B,且 与双曲线C恒有两个不同的交点A和B,且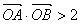 (其中O为原点),求k的取值范围. (其中O为原点),求k的取值范围.
[答案]
20、已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且 .过A、B两点分别作抛物线的切线,设其交点为M. .过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明 为定值; 为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
[答案]
|