1.设锐角θ使关于x的方程x2+4xcosθ+cotθ=0有重根,则θ的弧度数为( )
A.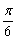 B.
B.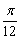 或
或
C.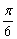 或
或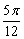 D.
D.
2.定义在R上的奇函数f(x)为减函数,设a+b≤0,给出下列不等式:
①f(a)·f(-a)≤0 ②f(b)·f(-b)≥0
③f(a)+f(b)≤f(-a)+f(-b) ④f(a)+f(b)≥f(-a)+f(-b)
其中正确的不等式序号是( )
A.①②④ B.①④
C.②④ D.①③
3.不等式组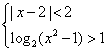 的解集为( )
的解集为( )
A.(0,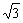 ) B.(
) B.(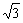 ,2)
,2)
C.(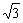 ,4) D.(2,4)
,4) D.(2,4)
4.曲线C:y=1+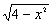 与直线l:y=k(x-2)+4有两个交点时实数k的取值范围是( )
与直线l:y=k(x-2)+4有两个交点时实数k的取值范围是( )
A.(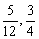 ] B.(
] B.(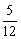 ,+∞)
,+∞)
C.(0,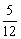 ) D.(
) D.(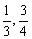 )
)
5.已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是( )
A.(0,1) B.(1,2)
C.(0,2) D.[2,+∞)
6.过x轴上一点P向圆C:x2+(y-2)2=1作切线,切点分别为A、B,则ΔPAB面积的最小值是( )
A.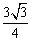 B.
B.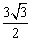
C.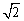 D.
D.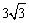
7.已知数列{an}中,a1=1,且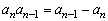 ,则a10=( )
,则a10=( )
A.10 B.8
C.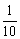 D.
D.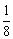
8.若实数x,y满足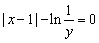 ,则y关于x的函数的图象大致是( )
,则y关于x的函数的图象大致是( )
9.设曲线y=x2与曲线y=-x2+x+1(x>0)在它们交点处的两切线的夹角为θ,则tanθ等于( )
A.3 B.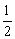
C.2 D.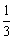
10.在正方体的8个顶点,12条棱的中点,6个面的中心及正方体的中心共27个点中,共线的三点组个数为( )
A.57 B.49
C.43 D.37
11.在直角坐标系中,设A(-2,3),B(3,-2),沿x轴把直角坐标系折成120°二面角后,则AB的长度是( )
A.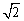 B.
B.
C.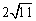 D.
D.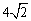
12.已知P是以F1、F2为焦点的椭圆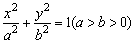 上一点,若PF1⊥PF2,tan∠PF1F2=
上一点,若PF1⊥PF2,tan∠PF1F2=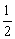 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A.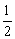 B.
B.
C.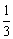 D.
D.
13.已知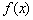 是定义在R上的奇函数,且是周期为2的周期函数,当
是定义在R上的奇函数,且是周期为2的周期函数,当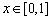 时,
时,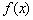 =2x-1,则
=2x-1,则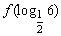 的值为( )
的值为( )
A.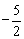 B.
B.
C.-5 D.-6
14.设四面体ABCD各棱长均相等,E、F分别为AC、AD的中点,则△BEF在该四面体ABCD上的射影是( )
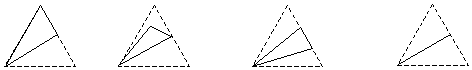
A. B. C. D.
15.函数y=lg[x2+(k+3)x+4]的值域为R,则实数k的取值范围是( )
A.-7≤k≤1 B.k≤-7或k≥1
C.-1≤k≤7 D.k<-7或k>1
16.6名同学报考A、B、C三所院校,如果每一所院校至少有1人报考,则不同的报考方法共有( )
A.216种 B.540种
C.729种 D.3240种
17.设三棱柱ABC—A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B—APQC的体积为( )

18.不等式|x+log3x|<|x|+|log3x|的解集是( )
A.(0,1) B.(0,+∞)
C.(1,+∞) D.(-∞,+∞)
19.双曲线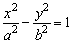 的一条准线被它的两条渐近线所截得的线段长度恰好等于它的一个焦点到一条渐近线的距离,则该双曲线的离心率为( )
的一条准线被它的两条渐近线所截得的线段长度恰好等于它的一个焦点到一条渐近线的距离,则该双曲线的离心率为( )
A.3 B.2
C. D.
D.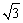
20.如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传送信息,信息可以分开沿不同的路线同时传送,则单位时间内传递的最大信息量为( )
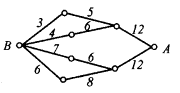
A.26 B.24
C.20 D.19