一、选择题
1.已知函数f(x)=loga[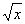 -(2a)2]对任意x∈[ -(2a)2]对任意x∈[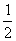 ,+∞)都有意义,则实数a的取值范围是( ) ,+∞)都有意义,则实数a的取值范围是( )
A.(0, 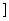 B.(0, B.(0,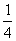 ) )
C.[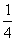 ,1 ,1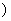 D.( D.(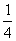 , ,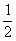 ) )
2.若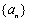 是等差数列,首项 是等差数列,首项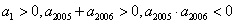 ,则使前 ,则使前 项和 项和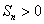 成立的最大自然数 成立的最大自然数 是( ) 是( )
A.4009 B.4010
C.4011 D.4012
3.已知函数y=f(x)有反函数,则方程f(x)=a(a是常数)应( )
A.有且仅有一个实根 B.至多有一个实根
C.至少有一个实根 D.不同于以上结论
4.定义域和值域均为 (常数 (常数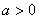 )的函数 )的函数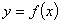 和 和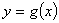 的图像如图所示,给出下列四个命题: 的图像如图所示,给出下列四个命题:
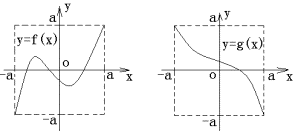
(1)方程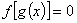 有且仅有三个解; 有且仅有三个解;
(2)方程 有且仅有三个解; 有且仅有三个解;
(3)方程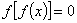 有且仅有九个解; 有且仅有九个解;
(4)方程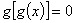 有且仅有一个解. 有且仅有一个解.
那么,其中正确命题的个数是( )
A.1 B.2
C.3 D.4
5.设函数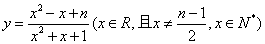 的最小值为 的最小值为 ,最大值为 ,最大值为 .若 .若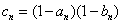 ,则数列 ,则数列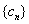 ( ) ( )
A.是公差不等于零的等差数列
B.是公比不等于1的等比数列
C.是常数列
D.不是等差数列也不是等比数列
6.设定义域为R的函数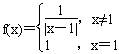 ,若关于x的方程f2(x)+bf(x)+c=0有3个不同的实数解x1、x2、x3,则 ,若关于x的方程f2(x)+bf(x)+c=0有3个不同的实数解x1、x2、x3,则 等于( ) 等于( )
A.5 B.
C.13 D.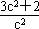
7.已知函数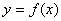 的图象与函数 的图象与函数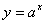 ( (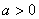 且 且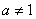 )的图象关于直线 )的图象关于直线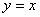 对称,记 对称,记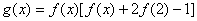 .若 .若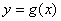 在区间 在区间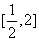 上是增函数,则实数 上是增函数,则实数 的取值范围是( ) 的取值范围是( )
A.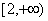 B. B.
C.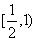 D. D.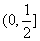
8.若 且 且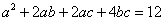 ,则 ,则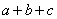 的最小值是( ) 的最小值是( )
A.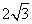 B.3 B.3
C.2 D.
9.关于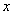 的方程 的方程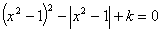 ,给出下列四个命题: ,给出下列四个命题:
①存在实数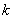 ,使得方程恰有2个不同的实根; ,使得方程恰有2个不同的实根;
②存在实数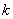 ,使得方程恰有4个不同的实根; ,使得方程恰有4个不同的实根;
③存在实数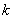 ,使得方程恰有5个不同的实根; ,使得方程恰有5个不同的实根;
④存在实数 ,使得方程恰有8个不同的实根. ,使得方程恰有8个不同的实根.
其中假命题的个数是( )
A. 0 B. 1
C. 2 D. 3
10.过双曲线M: 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B、C,且 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B、C,且 ,则双曲线M的离心率是( ) ,则双曲线M的离心率是( )
A.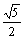 B. B. 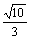
C. 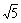 D. D. 
[提示]
二、填空题
11.关于x的方程lg(ax-1)-lg(x-3)=1有解,则a的取值范围是___________.
12.x0是x的方程ax=logax(0<a<1)的解,则x0,1,a这三个数的大小关系是___________.
13.已知a,b为常数,若 则 则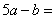 ___________. ___________.
14.设f(x)=log3(x+6)的反函数为f-1(x),若[f-1(m)+6][f-1(n)+6]=27,则f(m+n)=__________________.
15.若关于 的方程 的方程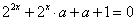 有实数解,则实数 有实数解,则实数 的取值范围是_________. 的取值范围是_________.
16.三个同学对问题“关于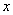 的不等式 的不等式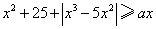 在 在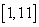 上恒成立,求实数 上恒成立,求实数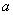 的范围”提出各自的解题思路: 的范围”提出各自的解题思路:
甲说:只需不等式左边最小值不小于右边最大值.
乙说:把不等式变形为左边含变量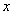 的函数,右边仅含常数,求函数最值. 的函数,右边仅含常数,求函数最值.
丙说:把不等式两边看成关于 的函数,作出函数的图像. 的函数,作出函数的图像.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即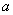 的范围是_________. 的范围是_________.
[答案]
三、解答题
17.已知f(x)=lg ,且f(1)=0,当x>0时,总有f(x)-f( ,且f(1)=0,当x>0时,总有f(x)-f(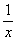 )=lgx. )=lgx.
(1)求f(x)的解析式;
(2)若方程f(x)=lg(m+x)的解集是 ,求实数m的取值范围. ,求实数m的取值范围.
[答案]
18.已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x-1)=f(3-x)且方程f(x)=2x有等根.
(1)求f(x)的解析式;
(2)是否存在实数m,n(m<n),使f(x)定义域和值域分别为[m,n]和[4m,4n],如果存在,求出m、n的值;如果不存在,说明理由.
[答案]
19.已知椭圆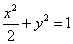 的左焦点为F,O为坐标原点. 的左焦点为F,O为坐标原点.
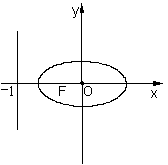
(1)求过点O、F,并且与椭圆的左准线 相切的圆的方程; 相切的圆的方程;
(2)设过点F的直线交椭圆于A、B两点,并且线段AB的中点在直线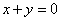 上,求直线AB的方程. 上,求直线AB的方程.
[答案]
20.对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+(b-1)(a≠0)
(1)若a=1,b=-2时,求f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B关于直线y=kx+ 对称,求b的最小值. 对称,求b的最小值.
[答案]
|