1、集合 ,若对于运算“
,若对于运算“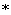 ”,若
”,若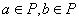 ,则
,则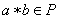 ,则运算“
,则运算“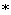 ”可以是( )
”可以是( )
A.加法 B.减法
C.除法 D.乘法
2、若非空集合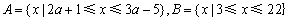 ,则能使
,则能使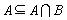 成立的所有a的集合是( )
成立的所有a的集合是( )
A. B.
B.
C. D.
D.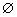
3、对于实数x,若n≤x<n+1(n∈Z)时,规定[x]=n,则不等式4[x]2-40[x]+75<0的解集是( )
A.[3,7] B.[3,8)
C.(2,7] D.(2,8)
4、设函数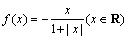 ,区间
,区间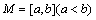 ,集合
,集合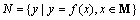 ,设使
,设使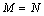 成立的实数对
成立的实数对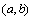 有( )
有( )
A.0个 B.1个
C.2个 D.无穷多个
5、定义两种运算: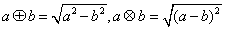 ,则函数
,则函数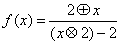 的解析式为( )
的解析式为( )
A.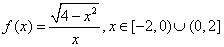
B.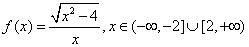
C.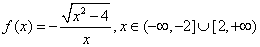
D.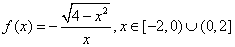
6、设M是具有以下性质的函数f(x)的全体:对于任意s>0,t>0,都有f(s)+f(t)<f(s+t).给出函数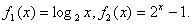 下列判断正确的是( )
下列判断正确的是( )
A. B.
B.
C. D.
D.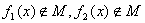
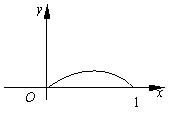
7、已知函数 (0≤x≤1)的图象的一段圆弧(如图所示),若
(0≤x≤1)的图象的一段圆弧(如图所示),若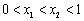 ,则( )
,则( )
A.
B.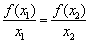
C.
D.当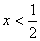 时
时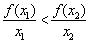 ,当
,当 ≥
≥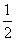 时
时
8、已知 是定义在R上的函数,
是定义在R上的函数, ,且对任意
,且对任意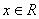 都有
都有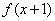 ≤
≤ ,
, ≥
≥ ,则
,则 的值是( )
的值是( )
A.6 B.5
C.7 D.不能确定
9、为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
A.4,6,1,7 B.7,6,1,4
C.6,4,1,7 D.1,6,4,7
10、f(x)是定义在区间[-c,c]上的奇函数,其图像如图所示. 令g(x)=a f(x)+b,则下列关于函数g(x)的叙述正确的是( )
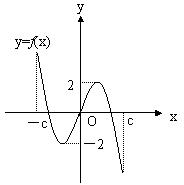
A.若a<0,b≠0,则函数g(x)的图象关于原点对称
B.若a=-1,-2<b<0,则方程g(x)=0有大于2的实根
C.若a≠0,b=2,则方程g(x)=0有两个实根
D.若a≥1,b<2,则方程g(x)=0有三个实根
11、含有三个实数的集合可表示为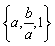 ,也可表示为{a2,a+b,0},则a2008+b2008的值为________.
,也可表示为{a2,a+b,0},则a2008+b2008的值为________.
12、若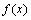 是奇函数,
是奇函数,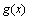 是偶函数,且
是偶函数,且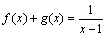 ,则
,则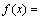 ________.
________.
13、设非空集合A={x|0≤x≤a}, B={y|y=2x+3,x∈A}, C={z|z=x2, x∈A},若B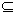 C,则实数a的取值范围为______________.
C,则实数a的取值范围为______________.
14、设函数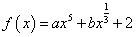 在区间
在区间 上的最大值为8,则
上的最大值为8,则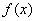 在区间
在区间 上的最小值为_________________.
上的最小值为_________________.
15、非空集合G关于运算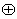 满足:(1)对任意的
满足:(1)对任意的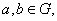 都有
都有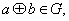 (2)存在
(2)存在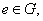 都有
都有 则称G关于运算
则称G关于运算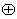 为“融洽集”.现给出下列集合和运算:
为“融洽集”.现给出下列集合和运算:
①G={非负整数},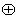 为整数的加法.
为整数的加法.
②G={偶数},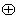 为整数的乘法.
为整数的乘法.
③G={平面向量},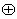 为平面向量的加法.
为平面向量的加法.
④G={二次三项式},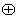 为多项式的加法.
为多项式的加法.
⑤G={虚数},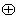 为复数的乘法.
为复数的乘法.
其中G关于运算 为“融洽集”的是_________。(填上所有你以为正确的选项序号)
为“融洽集”的是_________。(填上所有你以为正确的选项序号)