一、选择题
1、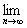 [n(1- [n(1-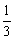 )(1- )(1-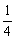 )(1- )(1-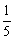 )…(1- )…(1-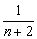 )]等于( ) )]等于( )
A.0 B.1
C.2 D.3
2、数列{an}中,a1=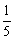 ,an+an+1= ,an+an+1=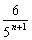 ,n∈N*,则 ,n∈N*,则 (a1+a2+…+an)等于( ) (a1+a2+…+an)等于( )
A.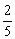 B. B.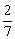
C.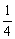 D. D.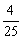
3、已知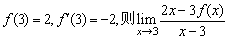 的值是( ) 的值是( )
A.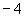 B.0 B.0
C.8 D.不存在
4、在函数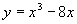 的图象上,其切线的倾斜角小于 的图象上,其切线的倾斜角小于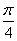 的点中,坐标为整数的点的个数是( ) 的点中,坐标为整数的点的个数是( )
A.3 B.2
C.1 D.0
5、设f0(x) = sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x) = fn′(x),n∈N,则f2005(x)=( )
A.sinx B.-sinx
C.cosx D.-cosx
6、已知对任意实数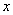 ,有 ,有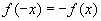 , ,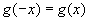 ,且 ,且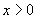 时, 时,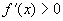 , ,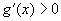 ,则 ,则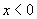 时( ) 时( )
A.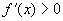 , ,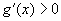
B.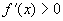 , ,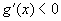
C.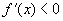 , ,
D. , ,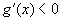
7、经过原点且与曲线y= 相切的方程是( ) 相切的方程是( )
A.x+y=0或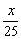 +y=0 B.x-y=0或 +y=0 B.x-y=0或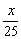 +y=0 +y=0
C.x+y=0或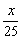 -y=0 D.x-y=0或 -y=0 D.x-y=0或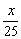 -y=0 -y=0
8、已知函数f(x)=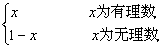 函数f(x)在哪点连续( ) 函数f(x)在哪点连续( )
A.处处连续 B.x=1
C.x=0 D.x=
9、已知二次函数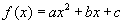 的导数为 的导数为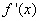 , , ,对于任意实数 ,对于任意实数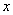 ,都有 ,都有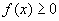 ,则 ,则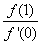 的最小值为( ) 的最小值为( )
A.3 B.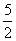
C.2 D.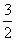
10、设函数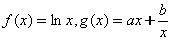 ,它们的图象在x轴上的公共点处有公切线,则当 ,它们的图象在x轴上的公共点处有公切线,则当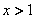 时, 时,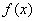 与 与 的大小关系是( ) 的大小关系是( )
A.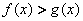 B. B.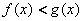
C.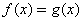 D. D.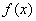 与 与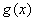 的大小不确定 的大小不确定
[提示]
二、填空题
11、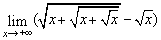 =__________. =__________.
12、曲线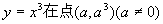 处的切线与x轴、直线 处的切线与x轴、直线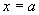 所围成的三角形的面积为 所围成的三角形的面积为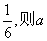 =__________. =__________.
13、设f(x)=x(x+1)(x+2)…(x+n),则f′(0)= __________.
14、若直线y=3x+1是曲线y=x3-a的一条切线,则实数a的值是_______.
15、函数y=f(x)的导函数的图象如下图所示,给出下列判断:
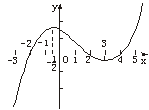
①函数y=f(x)在区间(-3,-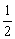 )内单调递增; )内单调递增;
②函数y=f(x)在区间(-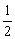 ,3)内单调递减; ,3)内单调递减;
③函数y=f(x)在区间(4,5)内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x=-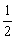 时,函数y=f(x)有极大值. 时,函数y=f(x)有极大值.
则上述判断中正确的是_____________.
16、已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(0,1),(2,0),如图所示.求:
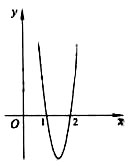
(Ⅰ)x0的值;
(Ⅱ)a,b,c的值.
[答案]
三、解答题
17、已知函数f(x)=x3+bx2+cx+d的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为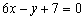 . .
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
[答案]
18、(08江苏卷17)某地有三家工厂,分别位于矩形ABCD 的顶点A,B 及CD的中点P 处,已知AB=20km,CB =10km,为了处理三家工厂的污水,现要在矩形ABCD 的区域上(含边界),且A,B 与等距离的一点O 处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
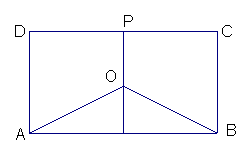
(Ⅰ)按下列要求写出函数关系式:
①设∠BAO= (rad),将y表示成 (rad),将y表示成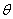 的函数关系式; 的函数关系式;
②设OP=x(km) ,将y表示成x的函数关系式.
(Ⅱ)请你选用(Ⅰ)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短.
[答案]
19、设数列a1,a2,…,an,…的前n项的和Sn和an的关系是Sn=1-ban-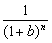 ,其中b是与n无关的常数,且b≠-1. ,其中b是与n无关的常数,且b≠-1.
(1)求an和an-1的关系式;
(2)写出用n和b表示an的表达式;
(3)当0<b<1时,求极限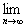 Sn. Sn.
[答案]
20、已知f(x)=ax-ln(-x),x∈[-e,0),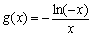 ,其中e=2.718 28…是自然对数的底数,a∈R. ,其中e=2.718 28…是自然对数的底数,a∈R.
(1)若a=-1,求f(x)的极值;
(2)求证:在(1)的条件下, ; ;
(3)是否存在实数a,使f(x)的最小值是3,如果存在,求出a的值;如果不存在,说明理由.
[答案]
|