一、选择题
1.已知向量 ( ) ( )
A.30° B.60°
C.120° D.150°
2.已知点M1(6,2)和M2(1,7),直线y=mx-7与线段M1M2的交点分有向线段M1M2的比为3∶2,则m的值为( )
A.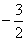 B. B.
C. D.4 D.4
3.已知a,b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是( )
A. B. B.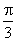
C.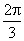 D. D.
4.已知向量 =(2,0),向量 =(2,0),向量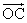 =(2,2),向量 =(2,2),向量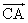 =( =(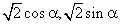 ),则向量 ),则向量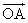 与向量 与向量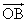 的夹角的范围为( ) 的夹角的范围为( )
A.[0,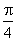 ] B.[ ] B.[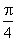 , , ] ]
C.[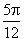 , ,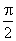 ] D.[ ] D.[ , ,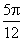 ] ]
5.设坐标原点为O,抛物线y2=2x与过焦点的直线交于A,B两点,则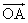 · · =( ) =( )
A.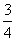 B. B.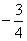
C.3 D.-3
6.O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足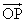 = =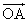 +λ( +λ(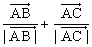 ), ), 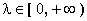 ,则点P的轨迹一定通过△ABC的( ) ,则点P的轨迹一定通过△ABC的( )
A.外心 B.内心
C.重心 D.垂心
7.点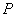 在平面上作匀速直线运动,速度向量 在平面上作匀速直线运动,速度向量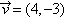 (即点 (即点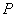 的运动方向与 的运动方向与 相同,且每秒移动的距离为 相同,且每秒移动的距离为 个单位).设开始时点P的坐标为(-10,10),则5秒后点P的坐标为( ) 个单位).设开始时点P的坐标为(-10,10),则5秒后点P的坐标为( )
A.(-2,4) B.(-30,25)
C.(10,-5) D.(5,-10)
8.已知向量 ≠ ≠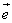 ,| ,|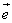 |=1,对任意t∈R,恒有| |=1,对任意t∈R,恒有|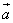 -t -t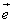 |≥| |≥| - -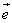 |,则( ) |,则( )
A.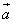 ⊥ ⊥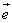 B. B.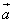 ⊥( ⊥(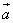 - -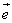 ) )
C.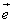 ⊥( ⊥(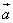 - - ) D.( ) D.( + +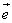 )⊥( )⊥( - - ) )
9.P是△ABC所在平面上一点,若 ,则P是△ABC的( ) ,则P是△ABC的( )
A.外心 B.内心
C.重心 D.垂心
10.△ABC中,若a4+b4+c4=2c2(a2+b2),则∠C度数是( )
A.60° B.45°或135°
C.120° D.30°
[提示]
二、填空题
11.已知a是以点A(3,-1)为起点,且与向量b = (-3,4)平行的单位向量,则向量a的终点坐标是__________.
12.如图,在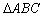 中, 中,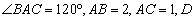 是边 是边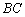 上一点, 上一点, 则 则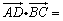 ______________. ______________.
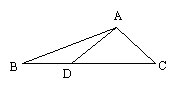
13.非零不共线向量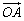 、 、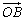 ,且2 ,且2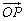 =m =m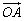 +2n +2n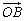 ,若 ,若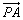 =λ =λ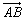 (λ∈R),则点Q(m,n)的轨迹方程是__________. (λ∈R),则点Q(m,n)的轨迹方程是__________.
14.已知平面上三点A、B、C满足|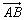 |=3,| |=3,|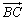 |=4,| |=4,| |=5,则 |=5,则 的值等于__________. 的值等于__________.
15.在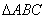 中,O为中线AM上一个动点,若AM=2,则 中,O为中线AM上一个动点,若AM=2,则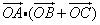 的最小值是_____. 的最小值是_____.
[答案]
三、解答题
16.已知向量a=(sinθ,1),b=(1,cosθ), . .
(Ⅰ)若a⊥b,求θ;
(Ⅱ)求|a+b|的最大值.
[答案]
17.(06年江西卷)如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设∠MGA=α( ). ).
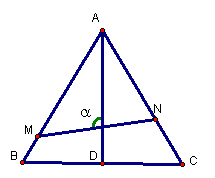
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数.
(2)求y=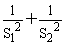 的最大值与最小值. 的最大值与最小值.
[答案]
18.已知定点F(1,0),动点P在y轴上运动,过点P作PM交x轴于点M,并延长MP至点N,且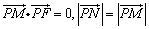 . .
(1)求动点N的轨迹方程;
(2)直线l与动点N的轨迹交于A、B两点,若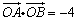 且4 且4 ≤ ≤ ≤ ≤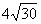 ,求直线l的斜率的取值范围. ,求直线l的斜率的取值范围.
[答案]
19.已知两点M(-1,0),N(1 ,0),且点P使 , ,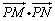 , ,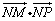 成公差小于零的等差数列. 成公差小于零的等差数列.
(Ⅰ)点P 的轨迹是什么曲线?
(Ⅱ)若点P坐标为(x0、y0),记θ为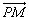 与 与 的夹角,求tanθ. 的夹角,求tanθ.
[答案]
20.已知点G是△ABC的重心,A(0,-1),B(0, 1),在x轴上有一点M,满足| |=| |=| |, |,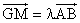 ( (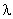 ∈R). ∈R).
(1)求点C的轨迹方程;
(2)若斜率为k的直线l与点C的轨迹交于不同两点P,Q,且满足| |=| |=|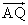 |,试求k的取值范围. |,试求k的取值范围.
[答案]
|