一、选择题
1、已知等差数列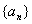 中, 中,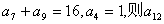 的值是( ) 的值是( )
A.15 B.30
C.31 D.64
2、已知在等差数列{ }中, }中,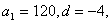 若 若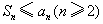 ,则n的最小值为( ) ,则n的最小值为( )
A.60 B.62
C.70 D.72
3、在等差数列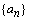 中, 中,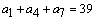 , , ,则数列 ,则数列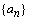 的前9项之和 的前9项之和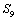 等于( ) 等于( )
A.66 B.99
C.144 D.297
4、设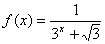 ,利用课本中推导等差数列前 ,利用课本中推导等差数列前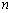 项和公式的方法,可求得 项和公式的方法,可求得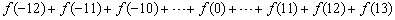 的值为( ) 的值为( )
A.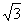 B. B.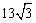
C.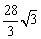 D. D.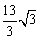
5、设f (n)为正整数n (十进制)的各数位上的数字的平方之和,比如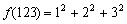 ,记f1(n) = f(n), ,记f1(n) = f(n),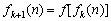 (k = 1,2,3,…),则 (k = 1,2,3,…),则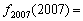 ( ) ( )
A.53 B.34
C.25 D.29
6、已知方程(x2-6x+k)(x2+6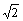 x+h)=0的4个实根经过调整后组成一个以2为首项的等比数列,则k+h=( ) x+h)=0的4个实根经过调整后组成一个以2为首项的等比数列,则k+h=( )
A.2-2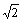 B.2+2 B.2+2
C.-6+6 D.24 D.24
7、如图,一个粒子在第一象限运动,在第一秒内,它从原点运动到 (0,1),然后它接着按图所示在x轴、y轴的平行方向来回运动(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,2)→…),且每秒移动一个单位长度,那么2008秒时,这个粒子所处位置为( )

A.(21,47) B.(20,48)
C.(44,20) D.(44,21)
8、用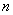 个不同的实数 个不同的实数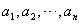 可得到 可得到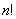 个不同的排列,每个排列为一行写成一个 个不同的排列,每个排列为一行写成一个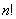 行的数阵.对第 行的数阵.对第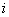 行 行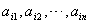 ,记 ,记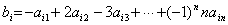 , ,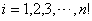 .例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以, .例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以, ,那么,在用1,2,3,4,5形成的数阵中, ,那么,在用1,2,3,4,5形成的数阵中,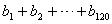 等于( ) 等于( )

A.—3600 B.1800
C.—1080 D.—720
9、设函数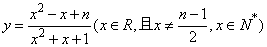 的最小值为 的最小值为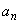 ,最大值为 ,最大值为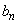 .若 .若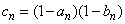 ,则数列 ,则数列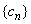 ( ) ( )
A.是公差不等于零的等差数列
B.是公比不等于1的等比数列
C.是常数列
D.不是等差数列也不是等比数列
10、在三棱锥A-BCD内部有2007个点,加上A、B、C、D四个顶点,共有2011个点,且任意三点不共线、任意四点不共面,将这2011个点中的任意四点连接起来构成小三棱锥,将三棱锥A-BCD分割成互不重叠的小三棱锥,则小三棱锥的个数为( )
A.6022 B.6020
C.6018 D.6015
[提示]
二、填空题
11、数列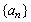 中, 中,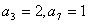 ,且数列 ,且数列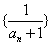 是等差数列,则 是等差数列,则 =___________. =___________.
12、已知某数列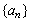 的公比为q,且前n项和为 的公比为q,且前n项和为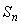 ,若集合 ,若集合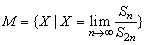 ,则M=___________. ,则M=___________.
13、已知数列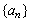 满足 满足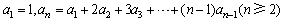 ,则 ,则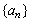 的通项公式 的通项公式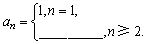
14、已知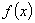 是定义在R上的不恒为零的函数,且对于任意的 是定义在R上的不恒为零的函数,且对于任意的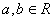 ,满足 ,满足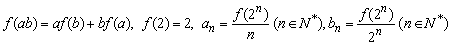
下列结论:①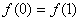 ;② ;②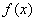 为偶函数;③数列 为偶函数;③数列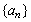 为等比数列;④数列 为等比数列;④数列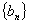 为等差数列.其中正确的是__________. 为等差数列.其中正确的是__________.
15、对大于或等于2的自然数m的n次幂进行如下方式的“分裂”
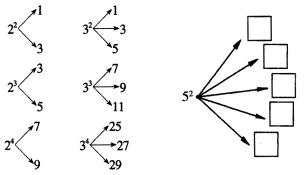
仿此,52的“分裂”中最大的数是__________,若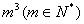 的“分裂”中最小的数是211,则m的值为__________。 的“分裂”中最小的数是211,则m的值为__________。
[答案]
三、解答题
16、设等比数列{an}的各项均为正数,项数是偶数,它的所有项的和等于偶数项和的4倍,且第二项与第四项的积是第3项与第4项和的9倍,问数列{lgan}的前多少项和最大?(lg2=0.3,lg3=0.4)
[答案]
17、设数列{an}前n项和为Sn=2n+n+1。
(1)求数列{an}的通项公式an.
(2)由数列{an}中奇数项a1,a3,a5,…构成一个新的数列{a2n-1},求{a2n-1}的前n项和。
[答案]
18、已知数列{an}满足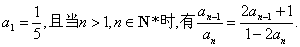
(1)求证:数列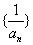 为等差数列; 为等差数列;
(2)试问a1a2是否是数列{an}中的项?如果是,是第几项;如果不是,请说明理由。
[答案]
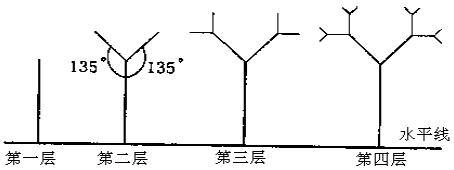
19、如图所示的树形图形.第一层是一条与水平线垂直的线段,长度为1;第二层在第一层线段的前端作两条与该段均成135°的线段,长度为其一半;第三层按第二层的方法在每一线段的前端生成两条线段;重复前面的作法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度.
(1)求第三层及第四层树形图的高度H3,H4;
(2)求第n层树形图的高度Hn;
(3)若树形图的高度大于2,则称树形图为“高大”,否则称为“矮小”.显然,当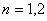 时是“矮小”的,是否存在 时是“矮小”的,是否存在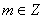 .使得当 .使得当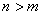 时,该树形图是“高大”的? 时,该树形图是“高大”的?
[答案]
20、对于数列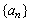 ,规定数列 ,规定数列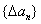 为数列 为数列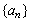 的一阶差分数列,其中 的一阶差分数列,其中 ;一般地,规定 ;一般地,规定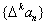 为 为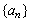 的k阶差分数列,其中 的k阶差分数列,其中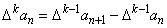 ,且 ,且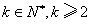 . .
(1)已知数列 的通项公式 的通项公式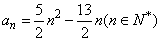 .试证明 .试证明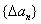 是等差数列; 是等差数列;
(2)若数列 的首项 的首项 ,且满足 ,且满足 ,求数列 ,求数列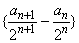 及 及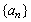 的通项公式; 的通项公式;
(3)在(2)的条件下,判断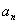 是否存在最小值,若存在求出其最小值,若不存在说明理由. 是否存在最小值,若存在求出其最小值,若不存在说明理由.
[答案]
|