一、选择题
1、某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过3小时,这种细菌由1个可繁殖成( )
A.511个 B.512个
C.1023个 D.1024个
2、两个完全相同的长方体的长、宽、高分别为5cm,4cm,3cm,把它们重叠在一起组成一个新长方体,在这些新长方体中,最长的对角线的长度是( )
A. B. B.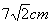
C.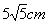 D. D.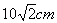
3、为确保信息安全,信息需加密传输,发送方由明文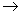 密文(加密),接收方由密文 密文(加密),接收方由密文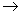 明文(解密),已知加密规则为:明文 明文(解密),已知加密规则为:明文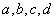 对应密文 对应密文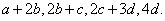 例如,明文 例如,明文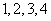 对应密文 对应密文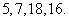 当接收方收到密文 当接收方收到密文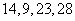 时,则解密得到的明文为( ) 时,则解密得到的明文为( )
A.7,6,1,4 B.6,4,1,7
C.4,6,1,7 D.1,6,4,7
4、某班试用电子投票系统选举班干部候选人.全班k名同学都有选举权和被选举权,他们的编号分别为1,2,…,k,规定:同意按“1”,不同意(含弃权)按“0”,令 其中i=1,2,…,k,且j=1,2,…,k,则同时同意第1,2号同学当选的人数为( ) 其中i=1,2,…,k,且j=1,2,…,k,则同时同意第1,2号同学当选的人数为( )
A.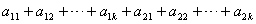
B.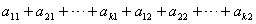
C.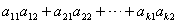
D.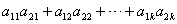
5、为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为( )
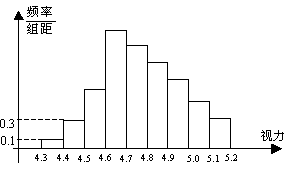
A.0.27,78 B.0.27,83
C.2.7,78 D.2.7,83
6、下图中有一个信号源和五个接收器.接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号.若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所有六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是( )
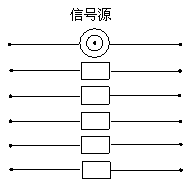
A.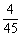 B. B.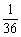
C.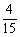 D. D.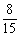
7、某厂生产甲产品每千克需用原料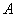 和原料 和原料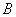 分别为 分别为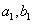 ,生产乙产品每千克需用原料 ,生产乙产品每千克需用原料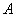 和原料 和原料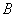 分别为 分别为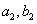 千克,甲、乙产品每千克可获利润分别为 千克,甲、乙产品每千克可获利润分别为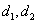 元,月初一次性购进本月用原料 元,月初一次性购进本月用原料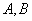 各 各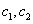 千克,要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月生产甲、乙两种产品分别为 千克,要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月生产甲、乙两种产品分别为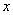 千克, 千克,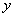 千克,月利润总额为 千克,月利润总额为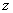 元,那么,用于求使总利润 元,那么,用于求使总利润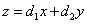 最大的数学模型中,约束条件为( ) 最大的数学模型中,约束条件为( )
A.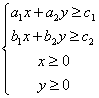 B. B.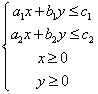
C.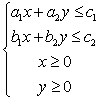 D. D.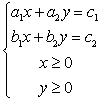
8、下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口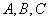 的机动车辆数如图所示(20,30;35,30;55,50),图中 的机动车辆数如图所示(20,30;35,30;55,50),图中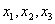 分别表示该时段单位时间通过路段 分别表示该时段单位时间通过路段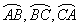 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( ) 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( )
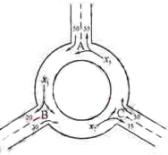
A.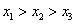 B. B.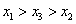
C.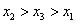 D. D.
9、某商场对顾客实行购物优惠活动,规定一次购物付款总额:(1)如果不超过200元,则不予优惠;(2)如果超过200元但不超过500元,则按标价给予9折优惠;(3)如果超过500元,其500元按第(2)条给予优惠,超过500元的部分给予7折优惠.某人两次去购物,分别付款168元和423元,假设他只去一次购买上述同样的商品,则应付款是( )
A.413.7元 B.513.7元
C.546.6元 D.548.7元
10、用长度分别为2,3,4,5,6 (单位:cm)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为( )
A.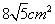 B. B.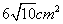
C.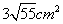 D. D.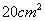
[提示]
二、填空题
11、将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形与圆的面积之和最小,正方形的周长应为__________.
12、某公司一年购买某种货物400吨,每次都购买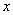 吨,运费为4万元/次,一年的总存储费用为 吨,运费为4万元/次,一年的总存储费用为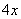 万元,要使一年的总运费与总存储费用之和最小,则x=______吨. 万元,要使一年的总运费与总存储费用之和最小,则x=______吨.
13、设坐标平面内有一个质点从原点出发,沿x轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动质点落在点(3,0)(允许重复过此点)处,则质点不同的运动方法共有__________种(用数字作答).
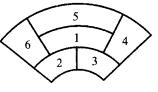
14、某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有__________.(以数字作答)
15、有一批材料可以围成200m长的围墙,现用此材料在一边靠墙的地方围成一块矩形场地,且内部用此材料隔成三个面积相等的矩形(如图),则围成的矩形场地的最大面积为__________.

[答案]
三、计算题
16、某集团公司为了获得更大的收益,每年要投入一定的资金用于广告促销.经调查,每投入广告费t(百万元),可增加销售额约为-t2+5t (百万元)(0≤t≤5).
(1)若该公司将当年的广告费控制在3百万元之内,则应投入多少广告费,才能使该公司由此获得的收益最大?
(2)现该公司准备共投入3百万元,分别用于广告促销和技术改造.经预测,每投入技术改造费x(百万元),可增加的销售额约为-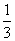 x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大?(注:收益=销售额-投入) x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大?(注:收益=销售额-投入)
[答案]
17、假设某市2004年新建住房400万平方米,其中有250万平方米是中低价房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底:
(1)该市历年所建中低价房的累计面积(以2004年为累计的第一年)将首次不少于4750万平方米?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?
[答案]
18、关于某港口今后20年的发展规划,有如下两种方案:
方案甲:按现状进行运营.据测算,每年可收入760万元,但由于港口淤积日益严重,从明年开始需投资进行清淤,第一年投资50万元,以后逐年递增20万元.
方案乙:从明年起开始投资6000万元进行港口改造,以彻底根治港口淤积并提高吞吐能力.港口改造需用时4年,在此期间边改造边运营.据测算,开始改造后港口第一年的收入为320万元,在以后的4年中,每年收入都比上一年增长50%,而后各年的收入都稳定在第5年的水平上.
(1)从明年开始至少经过多少年,方案乙能收回投资(累计总收益为正数)?
(2)从明年开始至少经过多少年,方案乙的累计总收益超过方案甲?(收益=收入-投资)
[答案]
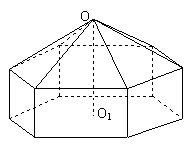
19、请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如下图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
[答案]
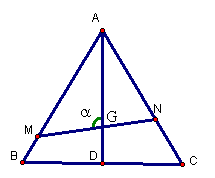
20、如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设△MGA=a(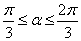 ),试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数,求 ),试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数,求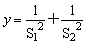 的最大值与最小值. 的最大值与最小值.
[答案]
|