一、选择题
1.方程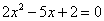 的两个根可分别作为( ) 的两个根可分别作为( )
A.一椭圆和一双曲线的离心率
B.两抛物线的离心率
C.一椭圆和一抛物线的离心率
D.两椭圆的离心率
2.双曲线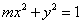 的虚轴长是实轴长的2倍,则 的虚轴长是实轴长的2倍,则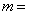 ( ) ( )
A.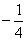 B.-4 B.-4
C.4 D.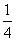
3.若抛物线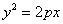 的焦点与椭圆 的焦点与椭圆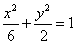 的右焦点重合,则 的右焦点重合,则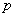 的值为( ) 的值为( )
A.-2 B.2
C.-4 D.4
4.已知双曲线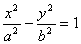 (a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( ) (a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.( 1,2) B. (1,2]
C.[2,+∞) D.(2,+∞)
5.已知双曲线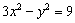 ,则双曲线右支上的点 ,则双曲线右支上的点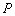 到右焦点的距离与点 到右焦点的距离与点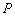 到右准线的距离之比等于( ) 到右准线的距离之比等于( )
A.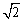 B. B. 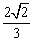
C. 2 D. 4
6.设过点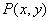 的直线分别与 的直线分别与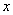 轴的正半轴和 轴的正半轴和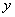 轴的正半轴交于 轴的正半轴交于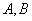 两点,点 两点,点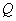 与点 与点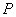 关于 关于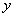 轴对称, 轴对称,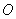 为坐标原点,若 为坐标原点,若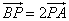 且 且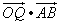 =1,则点 =1,则点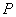 的轨迹方程是( ) 的轨迹方程是( )
A.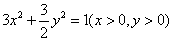 B. B.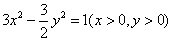
C.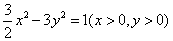 D. D.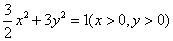
7.已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,满足 =0,则动点P(x,y)的轨迹方程为( ) =0,则动点P(x,y)的轨迹方程为( )
A. B. B.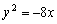
C. D. D.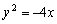
8.设O为坐标原点,F为抛物线y2=4x的焦点,A是抛物线上一点,若 =-4,则点A的坐标是( ) =-4,则点A的坐标是( )
A.(2,±2 ) B. (1,±2) ) B. (1,±2)
C.(1,2) D.(2,2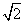 ) )
9.已知双曲线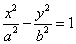 (a>0,b>0)的一条渐近线为y=kx(k>0),离心率e= (a>0,b>0)的一条渐近线为y=kx(k>0),离心率e=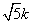 ,则双曲线方程为( ) ,则双曲线方程为( )
A.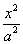 - -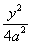 =1 B. =1 B.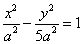
C.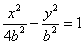 D. D.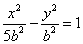
10.设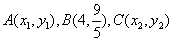 是右焦点为 是右焦点为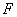 的椭圆 的椭圆 上三个不同的点,则“ 上三个不同的点,则“ 成等差数列”是“ 成等差数列”是“ ”的( ) ”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既非充分也非必要条件
[提示]
二、填空题
11.已知 为双曲线 为双曲线 的两个焦点, 的两个焦点, 为双曲线右支上异于顶点的任意一点, 为双曲线右支上异于顶点的任意一点, 为坐标原点.下面四个命题: 为坐标原点.下面四个命题:
A. 的内切圆的圆心必在直线 的内切圆的圆心必在直线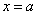 上; 上;
B.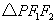 的内切圆的圆心必在直线 的内切圆的圆心必在直线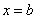 上; 上;
C. 的内切圆的圆心必在直线 的内切圆的圆心必在直线 上; 上;
D.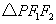 的内切圆必通过点 的内切圆必通过点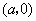 . .
其中真命题的代号是___________(写出所有真命题的代号).
12.已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值是___________.
13.双曲线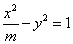 上的点到左焦点的距离与到左准线的距离的比是3,则m 等于___________. 上的点到左焦点的距离与到左准线的距离的比是3,则m 等于___________.
14.若曲线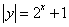 与直线 与直线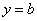 没有公共点,则 没有公共点,则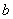 的取值范围是_________. 的取值范围是_________.
15.如图,把椭圆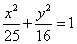 的长轴 的长轴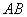 分成 分成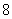 等份,过每个分点作 等份,过每个分点作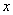 轴的垂线交椭圆的上半部分于 轴的垂线交椭圆的上半部分于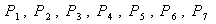 七个点, 七个点,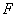 是椭圆的一个焦点,则 是椭圆的一个焦点,则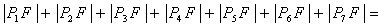 ___________. ___________.
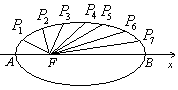
[答案]
三、解答题
16.如图,F为双曲线C: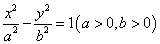 的右焦点.P为双曲线C右支上一点,且位于 的右焦点.P为双曲线C右支上一点,且位于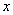 轴上方,M为左准线上一点, 轴上方,M为左准线上一点,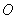 为坐标原点.已知四边形 为坐标原点.已知四边形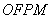 为平行四边形, 为平行四边形,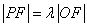 . .
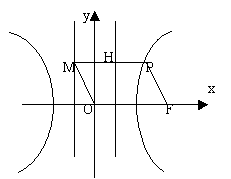
(Ⅰ)写出双曲线C的离心率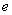 与 与 的关系式; 的关系式;
(Ⅱ)当 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若 ,求此时的双曲线方程. ,求此时的双曲线方程.
[答案]
17.在直角坐标系xOy中,已知圆心在第二象限、半径为2 的圆C与直线y=x相切于坐标原点O.椭圆 的圆C与直线y=x相切于坐标原点O.椭圆 与圆C的一个交点到椭圆两焦点的距离之和为10. 与圆C的一个交点到椭圆两焦点的距离之和为10.
(1)求圆C的方程;
(2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段OF的长,若存在,求出Q的坐标;若不存在,请说明理由.
[答案]
18.椭圆 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥PF2,|PF1|= 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥PF2,|PF1|= ,| PF2|= ,| PF2|= . .
(I)求椭圆C的方程;
(II)若直线l过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线l的方程.
[答案]
19.已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且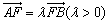 .过A、B两点分别作抛物线的切线,设其交点为M. .过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明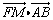 为定值; 为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
[答案]
20.已知一列椭圆Cn:x2+ =1.0<bn<1,n=1,2……若椭圆C上有一点Pn,使Pn到右准线ln的距离d是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点. =1.0<bn<1,n=1,2……若椭圆C上有一点Pn,使Pn到右准线ln的距离d是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点.
(Ⅰ)试证:bn≤ (n≥1); (n≥1);
(Ⅱ)取bn= ,并用Sn表示ΔPnFnGn的面积,试证: ,并用Sn表示ΔPnFnGn的面积,试证: (n≥3). (n≥3).
[答案]
|