一、选择题
1、如果实数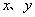 满足条件 满足条件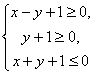 那么 那么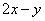 的最大值为( ) 的最大值为( )
A.2 B.1
C.-2 D.-3
2、直线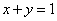 与圆 与圆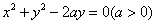 没有公共点,则 没有公共点,则 的取值范围是( ) 的取值范围是( )
A. B. B.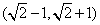
C.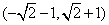 D. D.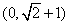
3、已知两条直线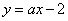 和 和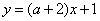 互相垂直,则a等于( ) 互相垂直,则a等于( )
A.2 B.1
C.0 D.-1
4、已知平面区域D由以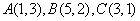 为顶点的三角形内部及边界组成.若在区域D上有无穷多个点 为顶点的三角形内部及边界组成.若在区域D上有无穷多个点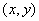 可使目标函数z=x+my取得最小值,则m=( ) 可使目标函数z=x+my取得最小值,则m=( )
A.-2 B.-1
C.1 D.4
5、以点(2,-1)为圆心且与直线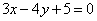 相切的圆的方程为( ) 相切的圆的方程为( )
A.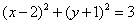 B. B.
C. D. D.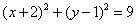
6、圆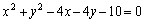 上的点到直线 上的点到直线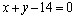 的最大距离与最小距离的差是( ) 的最大距离与最小距离的差是( )
A.36 B.18
C.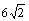 D. D.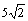
7、从圆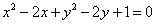 外一点 外一点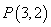 向这个圆作两条切线,则两切线夹角的余弦值为( ) 向这个圆作两条切线,则两切线夹角的余弦值为( )
A.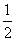 B. B.
C.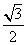 D.0 D.0
8、设直线过点(0,a),其斜率为1,且与圆x2+y2=2相切,则a 的值为( )
A.± B.±2 B.±2
B.±2 D.±4 D.±4
9、某厂生产甲产品每千克需用原料A和原料B分别为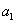 、 、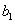 千克,生产乙产品每千克需用原料A和原料B分别为 千克,生产乙产品每千克需用原料A和原料B分别为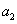 、 、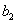 千克.甲、乙产品每千克可获利润分别为 千克.甲、乙产品每千克可获利润分别为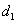 、 、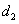 元.月初一次性购进本月用原料A、B各 元.月初一次性购进本月用原料A、B各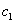 、 、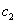 千克.要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大.在这个问题中,设全月生产甲、乙两种产品分别为 千克.要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大.在这个问题中,设全月生产甲、乙两种产品分别为 千克、 千克、 千克,月利润总额为 千克,月利润总额为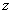 元,那么,用于求使总利润 元,那么,用于求使总利润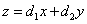 最大的数学模型中,约束条件为( ) 最大的数学模型中,约束条件为( )
A. B. B.
C. D. D.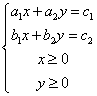
10、在平面直角坐标系中,不等式组 表示的平面区域的面积是( ) 表示的平面区域的面积是( )
A. B.4 B.4
C. D.2 D.2
[提示]
二、填空题
11、已知点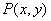 的坐标满足条件 的坐标满足条件 ,点O为坐标原点,那么|PO|的最小值等于_______,最大值等于____________. ,点O为坐标原点,那么|PO|的最小值等于_______,最大值等于____________.
12、若直线y=kx+2与圆(x-2)2+(y-3)2=1有两个不同的交点,则k 的取值范围是__________.
13、若半径为1的圆分别与 轴的正半轴和射线 轴的正半轴和射线 相切,则这个圆的方程为__________. 相切,则这个圆的方程为__________.
14、已知圆M:(x+cosθ)2+(y-sinθ)2=1,直线l:y=kx,下面四个命题:
(A)对任意实数k与θ,直线l和圆M相切;
(B)对任意实数k与θ,直线l和圆M有公共点;
(C)对任意实数θ,必存在实数k,使得直线l与和圆M相切
(D)对任意实数k,必存在实数θ,使得直线l与和圆M相切
其中真命题的代号是______________(写出所有真命题的代号)
15、已知变量x,y满足约束条件1≤x+y≤4,-2≤x-y≤2.若目标函数z=ax+y(其中a>0)仅在点(3,1)处取得最大值,则a的取值范围为___________.
[答案]
三、解答题
16、如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得 ,试建立适当的坐标系,并求动点 P的轨迹方程. ,试建立适当的坐标系,并求动点 P的轨迹方程.
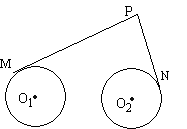
[答案]
17、已知圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3︰1;③圆心到直线l:x-2y=0的距离为 .求该圆的方程. .求该圆的方程.
[答案]
18、在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量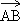 的坐标; 的坐标;
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
(3)是否存在实数a,使抛物线y=ax2-1上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求a的取值范围.
[答案]
19、已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点,(1)如果|AB|=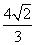 ,求直线MQ的方程;(2)求动弦AB的中点P的轨迹方程. ,求直线MQ的方程;(2)求动弦AB的中点P的轨迹方程.
[答案]
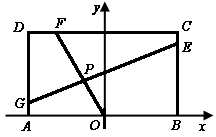
20、已知常数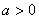 ,在矩形ABCD中, ,在矩形ABCD中,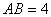 , ,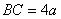 ,O为AR的中点,点E、F、G分别在BC、CD、DA上移动,且 ,O为AR的中点,点E、F、G分别在BC、CD、DA上移动,且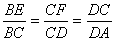 ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由. ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
[答案]
|