(一)电磁感应中的力学问题的分析方法
电磁感应中产生的感应电流在磁场中将受到安培力的作用,因此,电磁感应问题往往跟力学问题联系在一起.解决这类电磁感应中的力学问题,不仅要应用电磁学中的有关规律,如楞次定律、法拉第电磁感应定律,左右手定则、安培力的计算公式等;还要应用力学中的有关规律、机械能守恒定律等.要将电磁学和力学的知识综合起来应用.
例1、如图所示,位于水平面内的两条平行导轨相距l=30m;电源电动势ε=6V,内阻不计,R =5Ω;金属棒ab置于导轨上,且与导轨垂直;整个装置放在图示方向的匀强磁场中,当闭合K后金属棒运动时所受摩擦阻力f=0.1N,求ab棒的最大速度vmax和vmax对应的磁应强度B(金属棒和导轨的电阻不计).
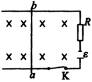
解析:
合上K后棒中电流由a到b,棒受到向左的磁场力做加速运动,因切割磁感线棒中产生由b向a的感应电动势.当棒的速度为v时,所受磁场力为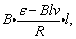 根据牛顿第二定律有: 根据牛顿第二定律有: . .
随着速度v的增大,加速度a减小,当a减为零时,速度达最大值,上式变为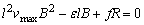
解得:
B有实数时,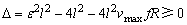 , ,
解得
可见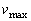 的最大值为: 的最大值为: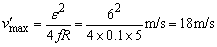
对应的磁感应强度为: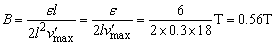
例2、如图所示,abcde和a′b′c′d′e′为两平行的光滑导轨,其中abcd和a′b′c′d′部分为处于水平面内的直轨,ab与a′b′的间距为cd与c′d′间距的2倍,de、d′e′部分与直轨相切的半径均为R的半圆形轨道.且处于竖直平面内.直轨部分处于竖直向上的匀强磁场中,弯轨部分处于匀强磁场外.在靠近aa′和cc′处分别放着两根金属棒MN、PQ,质量分别为2m和m为使棒PQ能沿导轨运动,且通过半圆形轨道的最高点ee′,在初始位置必须至少给棒MN以多大的冲量(设两段水平直轨均足够长,PQ出磁场时MN仍在宽轨道上运动.)

解析:
若棒PQ通过半圆形轨道最高点ee′,则由 可得其在最高点时的速度 可得其在最高点时的速度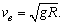
棒PQ在半圆形轨道上运动时机械能守恒,设其在dd′时的速度为vd,由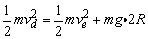
可得
两棒在直轨上运动的开始阶段,由于回路上存在感应电流,受安培力作用,棒MN速度减小,棒PQ速度增大.当棒MN的速度v1和棒PQ的速度v2达到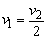 时,回路中磁通量不再变化而无感应电流,两都便做匀速运动, 时,回路中磁通量不再变化而无感应电流,两都便做匀速运动,
因而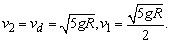
在有感应电流存在时的每一瞬间,由F=IBL及MN为PQ长度的2倍可知,棒MN和PQ所受安培力F1和F2有关系
设棒MN的初速度为v0,在时间t内分别对两棒应用动量定理,有:
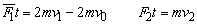
将以上两式相除,考虑到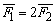 ,并将v1、v2的表达式代入.可得: ,并将v1、v2的表达式代入.可得: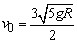
从而,至少应给棒MN的冲量
本例综合应用了电磁感应和圆周运动、机械能守恒和动量定理等多方知识.解答此类问题是提高综合应用知识能力的有效措施.
(二)电磁感应中电路问题的分析方法
在电磁感应中,切割磁感线的导体或磁通量发生变化的回路将产生感应电动势,该导体或回路就相当于电源.将它们接上电容器,便可使电容器充电;将它们接上电阻等用电器,便可对用电器供电,在回路中形成电流.因此,电磁感应问题又往往跟电路问题联系在一起,解决这类电磁感应中的电路问题,不仅要应用电磁学中的有关规律,如右手定则、楞次定律和法拉第电磁感应定律等;还要应用电路中的有关规律,如欧姆定律、串并联电路的性质等.要将电磁学和电路的知识甚至和力学知识综合起来应用.
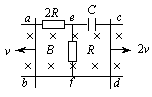
例3、如图,两个电阻器的阻值分别为R与2R,其余电阻不计,电容器电容量为C.匀强磁场磁感应强度的大小为B,方向垂直纸面向里.金属棒ab、cd的长度均为l.当棒ab以速度v,向左切割磁感线运动,金属棒cd以速度2v向右切割磁感线运动时,电容C的电量为多大?哪一个极板带正电?
解析:
金属棒ab以速度v向左切割磁感线运动,产生的感应电动势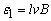 ,形成沿abfea方向的电流,电流强度为: ,形成沿abfea方向的电流,电流强度为: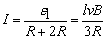
R两端电压为:
金屑棒cd以速度2v向右切割磁感线运动时,产生的感应电动势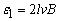 ,且c点电势高.由于cd所在回路不闭合,所以 ,且c点电势高.由于cd所在回路不闭合,所以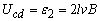
因为d、f两点等电势,所以: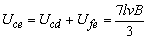
且c点电势高,从而,电容器C上的带电量为: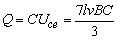
右侧极板带正电.
(三)电磁感应现象中能量转化问题的分析方法
导体切割磁感线或磁通量发生变化而在回路中产生感应电流,机械能或其它形式的能量便转化为电能;感应电流在磁场中受到安培力的作用或通过电阻发热,又可使电能转化为机械能或电阻的内能等;因此,电磁感应的过程总是伴随着能量转化的过程.对于某些电磁感应问题,我们可以从能量转化的观点出发,运用能量转化和守恒定律,运用功能关系分析解决.
例4、一电阻为R1的匀质光滑金属环竖直放置.一根电阻为r、长为l的轻质金属杆可绕环中心O无摩擦地转动,两端各固定一个金属球并套在环上可沿环滑动.球的质量分别为M、m,且M>m.Oa为一导线.连结金属杆O点和金属环a点并沿水平方向,电阻为R2、把杆从水平位置由静止释放,杆转至竖直位置时的角速度ω,如图(1)所示.试求:
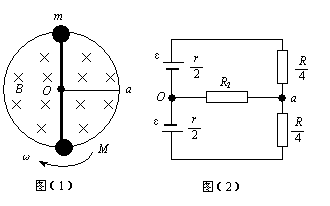
①杆转至竖直位置时,回路中电流的即时功率.
②杆从水平位置转至竖直位置的过程中,回路产生的焦耳热.
解析:
①杆转至竖直位置时,根据电路的对称性可知两球电势相等,左半环中无电流,等效电路如图(2)所示.从而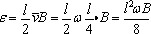
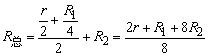
所以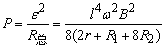
②由能量守恒可得: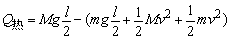
而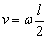 ,所以 ,所以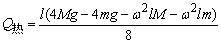
(四)电磁感应现象中的图象问题的分析方法
电磁感应中常涉及感应强度B、磁通量Ф、感应电动势ε和感应电流I随时间t变化的图象,即B—t图象、Ф—t图象、ε—t图象和I—t图象.对于切割产生感应电动势和感应电流的情况,还常涉及感应电动势ε和感应电流I随线圈位移x变化的图象,即ε—x图象和I—x图象.这些图象问题大体上可分为两类:由给定的电磁感应过程选出或画出正确的图象,或由给定的有关图象分析电磁感应过程,求解相应的物理量.不管是何种类型,电磁感应中的图象问题常需利用右手定则、楞次定律和法拉第电磁感应定律等规律分析解决.
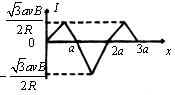
例5、如图所示,一个边长为a、电阻为R的等边三角线框,在外力作用下以速度v匀速地穿过宽度均为a的两个匀强磁场,这两个磁场的磁感应强度大小均为B,方向相反线框运动方向与底边平行且与磁场边缘垂直.取逆时针方向的电流为正,试通过计算,画出从图示位置开始,线框中产生的感应电流I与沿运动方向的位移x之间的函数图象.
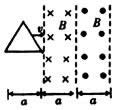
解析:
线框进入第一个磁场时,切割磁感线的有效长度在均匀变化.在位移由0到 过程中,切割有效长度由0增到 过程中,切割有效长度由0增到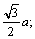 在位移由 在位移由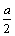 到a过程中,切割有效长度由 到a过程中,切割有效长度由 减到0、在 减到0、在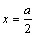 时, 时,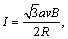 电流为正. 电流为正.
线框穿越两磁场边界时,线框在两磁场中切割磁感线产生的感应电动势相等且同向,切割的有效长度也在均匀变化.在位移由a到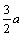 过程中,切割有效长度由0增到 过程中,切割有效长度由0增到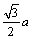 ;在位移由 ;在位移由 到2a过程中,切割有效长度由 到2a过程中,切割有效长度由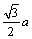 减到0、在a= 减到0、在a= 时, 时,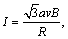 电流为负. 电流为负.
线框移出第二个磁场时的情况与进入第—个磁场相似.
可见,所求I—x图象应如图所示.
例6、如图(1)所示,截面积为0.2m2的100匝圆形线圈A处在变化磁场中,磁场方向垂直线圈截面,其磁感应强度B随时间t的变化规律如图(2)所示.设向外为B的正方向,线圈A上的箭头为感应电流I的正方向,R1=4Ω,R2=6Ω,C=30μF,线圈内阻不计.求电容器充电时的电压和2s后电容器放电的电量.

图(1) 图(2)
解析:
由题给B—t图象可知,在0~1s内,B为负值,表示其方向向里,B在逐渐减小,由楞决定律可知线圈中将产生顺时针方向的感应电动势;在1~2s内,B为正值,表示其方向向外,B在逐渐增大,同样由楞次定律可知线圈中仍将产生顺时针方向的感应电动势.在0~2s内,线圈A与电阻R1、R2组成闭合回路,回路中有感应电流,此时,电容器C处于充电状态.由题给B—t 图象,可知磁感应强度的变化率为: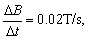 线圈A中的感应电动势为: 线圈A中的感应电动势为: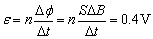 . .
通过R2的电流强度为
电容器C上的电压即为R2两端的电压.所以: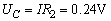
2s后磁场消失(B=0),电容器通过电阻和线圈放电;放电的电量即为充电后电容器上的带电量,所以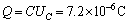 . .
(五)感应电动势大小的计算
1、平动切割磁感线类型
(1)计算公式: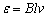
(2)说明:
①上式仅适用于导体各点以相同速度在匀强磁场中切割磁感线的情况,并且必须l、v与B两两垂直.
②若直线导线与v、B不两两垂直,则应取l、v、B互相垂直的分量.可见,当l、v、B两两垂直时,感应电动势最大;当l、v、B中任意两个量的方向相互平行时,感应电动势为零.
③若导线是曲折的,则l应是导线的有效切割长度.即是导线两端点在v、B所决定平面的垂线上的投影间的长度.
④公式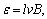 若v为一段时间内的平均值,则ε亦为该段时间内的平均值;若v为即时值,则ε亦为相应的瞬时值. 若v为一段时间内的平均值,则ε亦为该段时间内的平均值;若v为即时值,则ε亦为相应的瞬时值.
例7、如图所示,垂直纸面向外的磁场强弱沿y方向不变,沿x方向均匀增加,变化率为1 T/m.有一长l =0.2m、宽0.1 m的矩形金属框以2m/s的速度沿x方向匀速运动,则金属框中的感应电动势多大?若金属框电阻为0.02Ω,为保持金属框匀速运动.需加多大的外力?
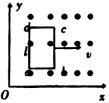
解析:
由于金属框的ad、bc两边切割磁感线,产生方向相反的感应电动势,所以框中总的感应电动势为:
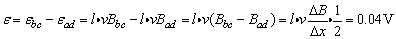
框中电流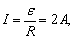 沿顺时针方向,bc边受向左的安培力 沿顺时针方向,bc边受向左的安培力 边受向右的安培力 边受向右的安培力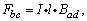 所以整个线框受培力 所以整个线框受培力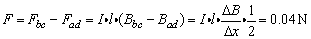 ,方向向左.为保持金属框匀速运动,需加0.04N的外力,方向向右. ,方向向左.为保持金属框匀速运动,需加0.04N的外力,方向向右.
2、磁通量发生变化类型
(1)计算公式:
(2)说明:
①上式适用于回路磁通量发生变化的情况,回路不一定要闭合.
②△ 不能决定ε的大小, 不能决定ε的大小,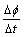 才能决定ε的大小,而 才能决定ε的大小,而 与△ 与△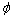 之间无大小上的必然联系. 之间无大小上的必然联系.
③当△ 仅由B的变化而引起时,则 仅由B的变化而引起时,则 .当△ .当△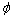 仅由S的变化引起时,则 仅由S的变化引起时,则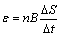 . .
④公式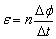 ,若△t取一段时间,则ε为△t这段时间内的平均值.当磁通量的变化 ,若△t取一段时间,则ε为△t这段时间内的平均值.当磁通量的变化 不是随时间线性变化时,平均电动势一般不等于初态与末态电动势的算术平均值.若△t趋近于零,则ε为瞬时值. 不是随时间线性变化时,平均电动势一般不等于初态与末态电动势的算术平均值.若△t趋近于零,则ε为瞬时值.
例8、如图所示,导线全部为裸导线,半径为r的圆内有垂直于圆平面的匀强磁场,磁感应强度为B.一根长度大于2r的导线MN以速度v在圆环上无摩擦地自左端匀速滑动到右端,电路的固定电阻为R,其余电阻忽略不计,试求NM从圆环的左端滑到右端的过程中电阻R上的电流强度的平均值及通过的电量.

解析:
本例粗看起来是MN在切割磁力线,属于“切割”类型,可用“切割式”求解,但MN的有效切割长度在不断变化,用“切割式”难以求得平均感应电动势.事实上,回路中的磁通量在不断变化,平均感应电动势可由磁通量变化式求得.
由于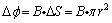 ,完成这一变化所用的时间为 ,完成这一变化所用的时间为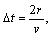 故 故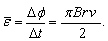 所以电阻R上的电流强度平均值为 所以电阻R上的电流强度平均值为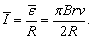
通过R的电量为: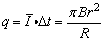
说明:若题中不要求感应电流的平均值.则通过导线横截面的电量可由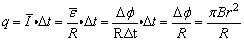 求得.一般地,对于n匝线圈的闭合回路,由于磁通量的变化而通过导线横截面的电量 求得.一般地,对于n匝线圈的闭合回路,由于磁通量的变化而通过导线横截面的电量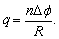
3、转动切割磁感线类型
(1)导线转动切割磁力线产生的感应电动势.此类问题通常可采用以下两种方法:
①运用公式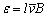 计算.式中l为导线转动切割磁力线的有效长度, 计算.式中l为导线转动切割磁力线的有效长度,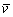 是导线上各点切割速度的平均值,l、 是导线上各点切割速度的平均值,l、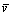 、B也应取互相垂直的分量. 、B也应取互相垂直的分量.
②运用公式 计算,式中△ 计算,式中△ 是导线在△t时间内切割的磁感线的条数. 是导线在△t时间内切割的磁感线的条数.
(2)线圈在匀强磁场中转动产生的感应电动势
①计算方法:线圈在磁场中转动产生的感应电动势可用公式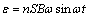 计算. 计算.
②几点说明:
 上式仅适用于线圈的转轴与线圈平面平行且与磁场垂直的情况,与线圈的形状及转轴相对于线圈的位置无关,且从线圈平面跟中性面重合时开始计时. 上式仅适用于线圈的转轴与线圈平面平行且与磁场垂直的情况,与线圈的形状及转轴相对于线圈的位置无关,且从线圈平面跟中性面重合时开始计时.
 由上式计算所得的是t时刻的感应电动势的瞬时值,在“交流电”一章中,感应电动势的瞬时值常用小写“e”表示,以区别于其有效值.线圈在磁场中转动产生的感应电动势的平均值则需由公式 由上式计算所得的是t时刻的感应电动势的瞬时值,在“交流电”一章中,感应电动势的瞬时值常用小写“e”表示,以区别于其有效值.线圈在磁场中转动产生的感应电动势的平均值则需由公式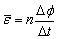 计算. 计算.
例9、如图所示,长l的金属导线下悬一小球,在竖直向下的匀强磁场中做圆锥摆运动,圆锥的半顶角为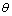 ,摆球的角速度为ω,磁感应强度为B,试求金属导线中产生的感应电动势. ,摆球的角速度为ω,磁感应强度为B,试求金属导线中产生的感应电动势.
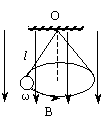
解析:
方法一:金属导线切割磁感线的有效长度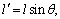 各点平均切割速度 各点平均切割速度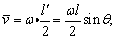 所以金属导线中产生的感应电动势 所以金属导线中产生的感应电动势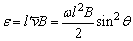 . .
方法二:金属线导线旋转一周切割的磁感线条数.即穿过圆锥底面的磁感线条数,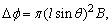 旋转一周所需的时间 旋转一周所需的时间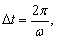 所以金属导线中产生的感应电动势 所以金属导线中产生的感应电动势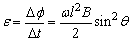 . .
- 返回 -
|