电磁学中科学应用问题，是物理学中的重点，也是学生学习的难点，又是高考中的热点。随着高中新课程计划的实施，高考改革的深化，这方面的问题依然是热门关注的焦点，往往以在科学技术中的应用的形式出现在问题的情景中，特别是近几年来此类问题在理科综合能力测试中频繁出现，现将此类问题分析如下：带电粒子在电磁场中的运动问题，主要有两大类，一类是利用电磁场的变化将其他信号转化为电信号，进而达到转化信息或自动控制的目的；另一类是利用电磁场对电荷或电流的作用，来控制其运动，使其平衡、加速、偏转或转动，已达到预定的目的。例如：
密立根实验—电场力与重力实验 |
速度选择器—电场力与洛伦兹力的平衡 |
直线加速器—电场的加速 |
质谱仪—磁场偏转 |
示波管—电场的加速和偏转 |
回旋加速器—电场加速、磁场偏转 |
电流表—安培力矩 |
电视机显像管—电场加速、磁场偏转 |
电动机—安培力矩 |
磁流体发电—电场力与洛伦兹力的平衡 |
霍尔效应—电场力与洛伦兹力作用下的偏转与平衡 |
磁流体发电机—电场力与洛伦兹力作用下的偏转与平衡 |
例1、（07年海南）据报道，最近已研制出一种可投入使用的电磁轨道炮，其原理如图所示。炮弹（可视为长方形导体）置于两固定的平行导轨之间，并与轨道壁密接。开始时炮弹在导轨的一端，通以电流后炮弹会被磁力加速，最后从位于导轨另一端的出口高速射出。设两导轨之间的距离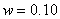
m，导轨长L＝5.0m，炮弹质量
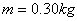。导轨上的电流I的方向如图中箭头所示。可以认为，炮弹在轨道内运动时，它所在处磁场的磁感应强度始终为Ｂ＝2.0Ｔ，方向垂直于纸面向里。若炮弹出口速度为
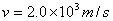，求通过导轨的电流I。忽略摩擦力与重力的影响。
解：在导轨通有电流Ｉ时，炮弹作为导体受到磁场施加的安培力为
Ｆ＝IwB ①
设炮弹的加速度的大小为a，则有
F=ma ②
炮弹在两导轨间做匀加速运动，因而
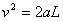③
联立①②③式得
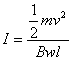④
代入题给数据得：
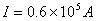⑤
例2、（07年北京卷）（18分）环保汽车将为2008年奥运会场馆服务。某辆以蓄电池为驱动能源的环保汽车，总质量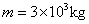
。当它在水平路面上以v=36km/h的速度匀速行驶时，驱动电机的输入电流I=50A，电压U=300V。在此行驶状态下
（1）求驱动电机的输入功率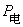
；
（2）若驱动电机能够将输入功率的90%转化为用于牵引汽车前进的机械功率P机，求汽车所受阻力与车重的比值（g取10m/s2）；
（3）设想改用太阳能电池给该车供电，其他条件不变，求所需的太阳能电池板的最小面积。结合计算结果，简述你对该设想的思考。
已知太阳辐射的总功率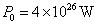
，太阳到地球的距离
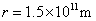，太阳光传播到达地面的过程中大约有30%的能量损耗，该车所用太阳能电池的能量转化效率约为15%。
解析：
（1）驱动电机的输入功率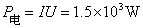
（2）在匀速行驶时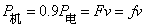
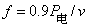
汽车所受阻力与车重之比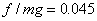
。
（3）当阳光垂直电磁板入射时，所需板面积最小，设其为S，距太阳中心为r的球面面积
。
若没有能量的损耗，太阳能电池板接受到的太阳能功率为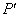
，则
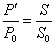
设太阳能电池板实际接收到的太阳能功率为P，
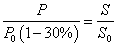
由于
，所以电池板的最小面积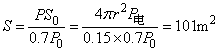
，分析可行性并提出合理的改进建议。
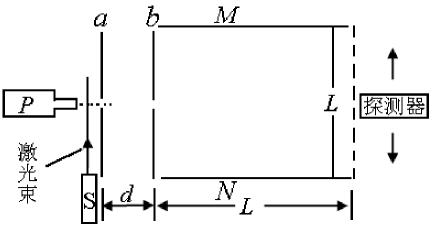
例3、（07年山东）飞行时间质谱仪可以对气体分子进行分析。如图所示，在真空状态下，脉冲阀P喷出微量气体，经激光照射产生不同价位的正离子，自a板小孔进入a、b间的加速电场，从b板小孔射出，沿中线方向进入M、N板间的偏转控制区，到达探测器。已知元电荷电量为e，a、b板间距为d，极板M、N的长度和间距均为L。不计离子重力及进入a板时的初速度。
（1）当a、b间的电压为U1时，在M、N间加上适当的电压U2，使离子到达探测器。请导出离子的全部飞行时间与比荷K（K=ne/m）的关系式。
（2）去掉偏转电压U2，在M、N间区域加上垂直于纸面的匀强磁场，磁感应强度B，若进入a、b间所有离子质量均为m，要使所有的离子均能通过控制区从右侧飞出，a、b间的加速电压U1至少为多少？
（1）由动能定理：neU1=1/2mv2
n价正离子在a、b间的加速度a1=neU1/md
在a、b间运动的时间t1=v/a1=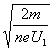
d
在MN间运动的时间：t2=L/v
离子到达探测器的时间：
t=t1＋t2=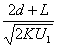
（2）假定n价正离子在磁场中向N板偏转，洛仑兹力充当向心力，设轨迹半径为R，由牛顿第二定律nevB=mv2/R
离子刚好从N板右侧边缘穿出时，由几何关系：
R2=L2＋(R－L/2)2
由以上各式得：U1=25neL2B2/32m
当n=1时U1取最小值Umin=25eL2B2/32m
例4、（07年山东）某压力锅结构如图所示。盖好密封锅盖，将压力阀套在出气孔上，给压力锅加热，当锅内气体压强达到一定值时，气体就把压力阀顶起。假定在压力阀被顶起时，停止加热。
（1）若此时锅内气体的体积为V，摩尔体积为V0，阿伏加德罗常数为NA，写出锅内气体分子数的估算表达式。
(2)假定在一次放气过程中，锅内气体对压力阀及外界做功1J,并向外界释放了2J的热量。锅内原有气体的内能如何变化？变化了多少？
（3）已知大气压强P随海拔高度H的变化满足P=P0（1－αH），其中常数α＞0。结合气体定律定性分析在不同的海拔高度使用压力锅，当压力阀被顶起时锅内气体的温度有何不同。
解：（1）设锅内气体分子数为n
n=V/V0·NA
（2）根据热力学第一定律
ΔE=W＋Q=－3J
锅内气体内能减少，减少了3J
（3）由P=P0（1－αH）（其中α＞0）知，随着海拔高度的增加，大气压强减小；
由P1=P＋mg/S知，随着海拔高度的增加，阀门被顶起时锅内气体压强减小；
根据查理定律P1/T1=P2/T2
可知阀门被顶起时锅内气体温度随着海拔高度的增加而降低。
例5、(07年天津)离子推进器是新一代航天动力装置，可用于卫星姿态控制和轨道修正。推进剂从图中P处注入，在A处电离出正离子，BC之间加有恒定电压，正离子进入B时的速度忽略不计，经加速后形成电流为I的离子束后喷出。已知推进器获得的推力为F，单位时间内喷出的离子质量为J。为研究问题方便，假定离子推进器在太空中飞行时不受其他外力，忽略推进器运动速度。
（1）求加在BC间的电压U；
（2）为使离子推进器正常运行，必须在出口D处向正离子束注入电子，试解释其原因。
解：
（1）设一个正离子的质量为m、电荷量为q，加速后的速度为v，根据动能定理，有
qU=
mv2
设离子推进器在Δt时间内喷出质量为ΔM的正离子，并以其为研究对象，推进器ΔM的作用力F′，由动量定理，有
F′Δt＝ΔMv
由牛顿第三定律知F′=F
设加速后离子束的横截面积为S，单位体积内的离子数为n，则有
I=nqvS J=nmvS
两式相比可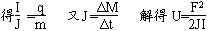
（2）推进器持续喷出正离子束，会使带有负电荷的电子留在其中，由于库仑力作用将来严重阻碍正离子的继续喷出，电子积累足够多时，甚至会将喷出的正离子再吸引回来，致使推进器无法正常工作。因此，必须在出口D处发射电子注入到正离子束，以中和正离子，使推进器获得持续推力。
从以上几例可知，讨论与电磁场有关的科技应用问题，首先应通过分析将其提炼成纯粹的物理问题，然后用解决物理问题的方法进行分析。这里较多的是用分析力学问题的方法；对于带电粒子在磁场中的运动，还特别应注意运用几何知识寻找关系。
解决实际问题的一般过程：
