|
一、重难点分析
1.电功和电热的区别
(1)纯电阻用电器:
①电流通过纯电阻用电器是以发热为目的,例如电炉、电熨斗、电饭锅、电铬铁、白炽灯泡等.
②在纯电阻电路中,电能全部转热能,电功等于电热.即:
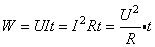
上述各式是通用的,没有区别.
同理: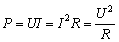 也无区别. 也无区别.
(2)非纯电阻用电器
①电流通过非纯电阻用电器是以转化为热能以外形式的能为目的,发热不是目的,而是不可避免的热能损失.如电动机、电解槽、给蓄电池充电、日光灯等.
②在非纯电阻电路中,电路消耗的电能,即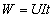 分为两部分,一大部分转化为其他形式的能(如电流通过电动机、电动机转动,电能转化为机械能);另一部分不可避免地转化为电热Q=I2Rt(电流通过电枢的电阻产生热).这时 分为两部分,一大部分转化为其他形式的能(如电流通过电动机、电动机转动,电能转化为机械能);另一部分不可避免地转化为电热Q=I2Rt(电流通过电枢的电阻产生热).这时 不再等于Q=I2Rt(而是W>Q),应该是 不再等于Q=I2Rt(而是W>Q),应该是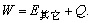 电功只能用 电功只能用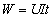 计算,电热只能用Q=I2Rt计算. 计算,电热只能用Q=I2Rt计算.
2.闭合电路的欧姆定律
(1)闭合电路的欧姆定律揭示了包含电源在内的闭合电路中,电流强度与电动势及电路总电阻之间的关系。
(2)定律内容及公式: . .
(3)适用范围:外电路是纯电阻的电路.
(4)路端电压随外电路电阻变化问题
路端电压的变化规律:
①与外电阻的变化关系(ε、r,不变):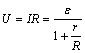
R |
增大 |
∞(断路) |
减小 |
0(短路) |
U |
增大 |
ε |
减小 |
0 |
I |
减小 |
0 |
增大 |

|
②与内阻的关系(ε、R不变):
r |
增大 |
∞(断路) |
减小 |
0 |
U |
减小 |
0 |
增大 |
ε |
I |
减小 |
0 |
增大 |
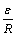
|
分析此类问题的基本思路是“抓住不变量,分析相关量”。抓住不变量是关键,在分析相关量变化时,要注意推理的逻辑顺序,要求分析中“步步有根据”。
(5)闭合电路的欧姆定律就是能的转化和守恒在闭合电路的反映
由ε=U+U′可得:εI=UI+U′I,即P总=P出+P内,在闭合电路的欧姆定律的应用中,要注意几种电功率的分辨。
(6)电源输出功率
电源的输出功率为: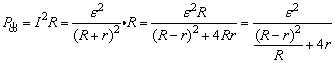
当R =r时,P出有最大值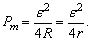
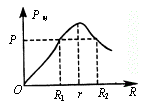
P出与外电阻R的这种函数关系可用图的图象定性地表示.由图象可知:对应于电源的非最大输出功率P可以有两个不同的外电阻R1、R2.由图象还可知:当R<r时,若R增加,P出增大;当R>r时,若R增大,则P出减小.值得注意的是上面的结论都是在电源的电动势ε和内电阻r不变的情况下适用.
(7)电源的效率:
电源的效率为: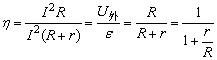
当R增大时,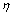 增大. 增大.
当R =r时,P出有最大值,而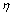 =50%. =50%.
3.U—I图象的物理意义
(1)部分电路
部分电路中任意导体两端电压与电流的关系为:U=IR
则U—I图象如图所示,其物理意义为:
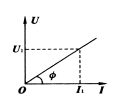
①描述导体两端电压U与电流强度的对应关系.
②斜率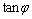 值表示导体电阻值,且斜率越大其电阻越大. 值表示导体电阻值,且斜率越大其电阻越大.
(2)闭合电路:
闭合电路的路端电压与电流的关系为:U=ε-Ir
则U—I图象如图所示,其物理意义为:
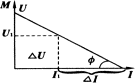
①描述路端电压与电流强度的对应关系;
②图线与U轴交点M的坐标值表示电源的电动势的值,反映外电路断开情况;
③图象与I轴交点N的坐标值表示短路电流(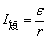 )的值; )的值;
④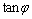 值表示电源内电阻值,注意:计算 值表示电源内电阻值,注意:计算 值时.若N点的电流强度对应的电压不为零(即电流值不是短路电流),则: 值时.若N点的电流强度对应的电压不为零(即电流值不是短路电流),则: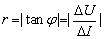
二、典型例题
(一)电路变化问题的分析方法
在直流电路中,当电键接通或断开时,改变电路结构时;或者移动滑动变阻器的滑片,改变某一部分电路的电阻时,电路中各部分的电流、电压和电功率都会随着变化.正确分析电路变化问题的方法是:
1.根据电路结构的变化情况,或者可变电阻值的变化情况,分析直流电路的总电阻的变化情况.下面是几个判断总电阻变化情况的规律:
(1)当外电路的任何一个电阻增大(减小)时,电路的总电阻一定增大(减小).
(2)若电键的通断使串联的用电器增多时,总电阻增大;若电键的通断使并联的支路增多时,总电阻减小.
(3)在图所示分压电路中,滑动变阻器可视为由两段电阻构成,其中一段与用电器并联(以下简称并联段),另一段与并联部分相串联(以下简称串联段);设滑动变阻器的总电阻为R,灯泡电阻为R灯,与灯泡并联的哪一段的电阻为R并,则分压器的总电阻为
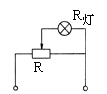
由上式看出,当R并减小时,R总增大;当R并增大时,R总减小.由此可以得出结论:分压器总电阻的变化情况,与并联段电阻的变化情况相反,与串联段电阻的变化情况相同.
2.根据全电路欧姆定律,分析总电流的变化情况和路端电压的变化情况,因为电源电动势和内阻均为定值,所以当外电阻R增大(或减小)时,由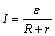 可知电流减小(或增大),由U =ε-Ir可知,路端电压随之增大(或流小). 可知电流减小(或增大),由U =ε-Ir可知,路端电压随之增大(或流小).
3.根据串、并联电路的特点和局部电流与整个电路的关系,分析各部分电路中的电流强度I、电压U和电功率P的变化情况,一般来说,应先分析定值电阻上的I、U、P的变化情况,后分析变化电阻上的I、U、P的变化情况.
例1、如图所示,当滑动变阻器的滑片P向上端移动时,判断电路中的电流表、电压表的示数如何变化?
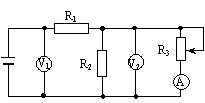
解析:
先认清 测R3中电流, 测R3中电流, 测R2、R3并联的电压, 测R2、R3并联的电压,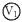 测路端电压. 测路端电压.
再利用欧姆定律分析判断主干电路上一些物理量的变化;P向上滑,R3的有效电阻增大,外电阻R外增大,干路电流I减小,路端电压U增大,至此,已判断出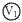 示数大. 示数大.
再进行分支电路上的分析:由I减小,知R1两端的电压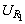 减小,由U外增大可知R2和R3并联的电压U2增大,断出的 减小,由U外增大可知R2和R3并联的电压U2增大,断出的 示数增大.由U2增大和R3有效电阻增大,无法确定 示数增大.由U2增大和R3有效电阻增大,无法确定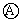 示效如何变化,这就要从另一条途径去分析:由 示效如何变化,这就要从另一条途径去分析:由 增大可知通过R2的电流I2增大,而干路电流I减小,所以R3中的电流减小,即 增大可知通过R2的电流I2增大,而干路电流I减小,所以R3中的电流减小,即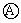 示数减小. 示数减小.
(二)含有电容器的电路的分析方法
电容器是一个储存电能的元件.在直流电路中,当电容器充、放电时,电路里有充、放电电流.一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑由电容器是理想的不漏电的情况)的元件,在电容器处电路可以看做是断路,简化电路时可去掉它.简化后若要计算电容器所带电量时,可在相应的位置补上.分析和计算含有电容器的直流电路时,应注意以下几点:
1.由于电容器所在支路无电流通过,所以在此支路中的电阻上无电压降,因此电容器两极间的电压等就等于该支路两端的电压.
2.当电容器和电阻并联后接入电路时,电容器两极间的电压与其并联电阻两端的电压相等.
3.几个电容器串联接入电路时,各电容器上所带电量相等.各个电容器上的电压之和等于电路的总电压,电容器上的电压与电容器的电容成反比,即:U1C1 = U2C2 = U3C3=……
例2、 如图所示,将一电动势ε=3V,内电阻不计的电源与阻值是30Ω、粗细均匀的、长度为30cm的电阻丝A、B相连.当滑动触头P以10cm/s的速度向右匀速滑动时,电流计的示数是多少?(已知电容器的电容为C=50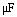 )流过电流计的电流方向如何? )流过电流计的电流方向如何?
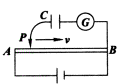
解析:
因为电源内阻不计,所以A、B两点间的电压为:UAB=ε=3V
在每秒钟内,P点向右移动10cm,电容器两极间的电压减小量为:
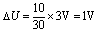
电容器的放电量为:△Q =C△U=50×10-6×1=5×10-5C
通过电流计的电流为: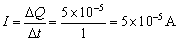
(三)电路故障的分析方法
1.故障的特点
(1)断路的特点:电路中发生断路,表现为电压不为零,而电流为零;若外电路中任意两点间的电压不为零,则这两点间有断点,而这两点与电源连接部分无断点.
(2)短路特点:电路中发生短路,表现为有电流通过电路而电压为零.
2.故障的分析方法
(1)仪器检测法:
①断点故障的判断:用电压表与电源并联,若有电压时,再逐段与电路并联,若电压表指针偏转,则该段电路中有断点.
②短路故障的判断:用电压表与电源并联,若有电压时,再逐段与电路并联,若电压表示数为零时,该电路被短路,当电压表示数不为零,则该电路不被短路或不完全被短路.
(2)假设法:
已知电路发生某种故障.寻求故障发生在何处时,可将整个电路划分为若干部分;然后逐一假设某部分电路发生故障,运用有关规律进行推理.推理结果若与题述现象不符.则故障不是发生在这部分电路;若推理结果与题述现象相符,则故障可能发生在这部分电路;直到找出发生故障的全部可能为止.
例3、图所示的电路中,电源电动势为6V,当开关K接通后,灯泡L1和L2,都不亮,用电压表测得各部分电压是Uab=6V,Uad=0V,Ucd=6V,由此可以断定( )
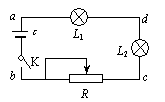
A.L1和L2灯丝都烧断了 B.L1的灯丝烧断了
C.L2的灯丝烧断了 D.变阻器R断路
解析:
由已知条件知:电路中有的地方有电压,可知电源有电压.由Uad =0可知a、d之间没有断点;由Uab=6V和Ucd=6V,可知外电路中的a、b之间没有断点,外电路中的c、d之间有断点;取公共部分,可知灯L2断路.由电灯L2两端的电压不为零.可知灯L1与变阻器R是导通的.
故本题应选C.
(四)电路中能量转化问题的分析方法
例4、一个用直流电动机提升重物的装置,如图所示.重物的质量m=50kg,电源的电动势ε=110V,不计电源内阻及各处的摩擦.当电动机以v=0.90m/s的恒定速度向上提升重物时,电路中的电流强度I =5A,由此可知电动机线圈的电阻R =________Ω.

解析:
由能的转化和守恒
即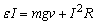 得 得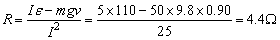
评析:
闭合电路中能的转化和守恒,由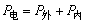 表述,其中 表述,其中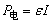 表示电源每秒产生的电能,P外=UI表示外电路每秒消耗的电能, 表示电源每秒产生的电能,P外=UI表示外电路每秒消耗的电能,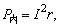 表示电源内部每秒消耗的电能,若外电路为纯电阻电路,则P外=I2R外.若外电路是非纯电阻电路,外电路消耗的电能转化为内能及其他形式的能,如本题中: 表示电源内部每秒消耗的电能,若外电路为纯电阻电路,则P外=I2R外.若外电路是非纯电阻电路,外电路消耗的电能转化为内能及其他形式的能,如本题中: (电源内部消耗的电能可忽略),这点在探索电路能量转化(电功率问题)时特别要注意. (电源内部消耗的电能可忽略),这点在探索电路能量转化(电功率问题)时特别要注意.
(五)直流电路的分析与计算
例5、如图所示的电路中,用电动势ε=6V,内阻不计的电池组向电阻R0=20Ω,额定电压U0=4.5V的灯泡供电.求:
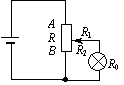
(1)要使系统的效率不低于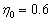 ,变阻器的阻值及它应承受的最大电流是多大? ,变阻器的阻值及它应承受的最大电流是多大?
(2)处于额定电压下的灯泡和电池组的最大可能效率是多少?它们同时适当选择的变阻器如何连接,才能取得最大效率?
解析:
(1)系统的效率为: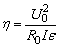
要使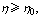 必有 必有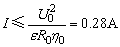
由题意知: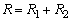
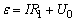
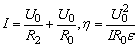
解方程组得: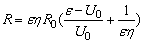
显然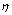 随R的增大而增大. 随R的增大而增大.
又因为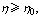 故 故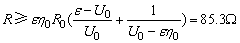
(2)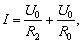 故 故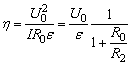
故当R2趋于无穷大,把变阻器的B端断开,使变阻器与灯泡串联时,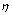 有极大值 有极大值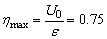
例6、 如图所示为一种测定风作用力的仪器原理图,P为球体,悬挂在一细长金属丝下面,O是悬挂点,R0是保护电阻,CD是水平放置的光滑电阻丝,与细金属丝始终保持良好接触,无风时细金属丝与电阻丝在C点接触,此时电路中电流为I0,有风时金属丝将偏转一角度,角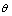 与风力大小有关,已知风力方向水平向左, 与风力大小有关,已知风力方向水平向左,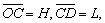 球的质量为m,电阻丝单位长度的阻值为k,电源内阻和金属丝电阻均不计,金属丝偏转 球的质量为m,电阻丝单位长度的阻值为k,电源内阻和金属丝电阻均不计,金属丝偏转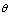 角时,电流表的示数为I′,此时风力大小为F,试写出: 角时,电流表的示数为I′,此时风力大小为F,试写出:
(1)风力大小F与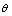 的关系式; 的关系式;
(2)风力大小F与电流表示数I′关系式.
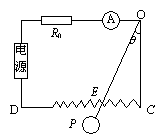
解题思路:
本题是测定风作用力的仪器,各量的制约关系是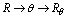 (DE电阻)→I,I随F的增大而增大,所以通过I可求风力F. (DE电阻)→I,I随F的增大而增大,所以通过I可求风力F.
解:
把“风力仪”抽象出两个模型,即单摆模型和电路模型见图.
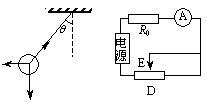
(1)以摆球为对象,它受三力而平衡,据平衡条件有
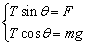 故 故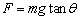 ① ①
(2)以电路为研究对象,据欧姆定律有
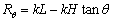 ② ②
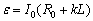 ③ ③
 ④ ④
联立①②③④解得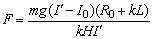 . .
评析:
本题属“理论联系实际”类型题,其基本结构是:①交待题源背景;②叙述过程原理;③设定题设条件;④提出具体问题,依据此种类型问题的结构特点,可以归纳出解决该题型的基本方法是“明确题意,弄通原理;建构模型,应用规律;推理计算,得出结论”.
例7、角速度计可测量航天器自转的角速度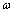 ,其结构如图所示,当系统绕OO′转动时,元件A在光滑杆上发生滑动,并输出电压信号成为航天器的制导信号源,已知A质量为m,弹簧的劲度系数为k,原长为L0,电源电动势为ε,内阻不计.滑动变阻器总长为L,电阻分布均匀,系统静止时滑动变阻器滑动头P在中点,与固定接点Q正对,当系统以角度速度 ,其结构如图所示,当系统绕OO′转动时,元件A在光滑杆上发生滑动,并输出电压信号成为航天器的制导信号源,已知A质量为m,弹簧的劲度系数为k,原长为L0,电源电动势为ε,内阻不计.滑动变阻器总长为L,电阻分布均匀,系统静止时滑动变阻器滑动头P在中点,与固定接点Q正对,当系统以角度速度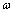 转动时,求: 转动时,求:
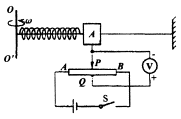
(1)弹簧形变量x与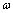 的关系式; 的关系式;
(2)电压表的示数U与角速度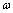 的函数关系. 的函数关系.
解析:
(1)当系统绕OO′以角速度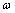 转动时,由牛顿第二定律有: 转动时,由牛顿第二定律有: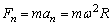
又因为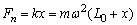 所以 所以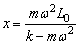
(2)由欧姆定律和串联分压原理可知: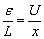
故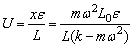
评析:
本题是力电综合的实际应用问题,抓住圆周运动规律和串联分压原理就迎刃而解了.
- 返回 -
|