下面就具体地学习力和三种最基本的力。
（一）力
1、力的概念：力是物体对物体的作用。可以理解为力不能离开物体而独立存在，有力就一定有“施力”和“受力”两个物体，二者缺一不可。
在力学中提到的研究对象就是指的受力物体。
2、力的作用效果：使物体发生形变或改变物体的运动状态(即使物体产物加速度)。
3、矢量性：既有大小又有方向。
(1)大小：可用弹簧秤称量，单位是牛顿(N)。
(2)方向：力作用的方向。
所以在表示力的时候要用到力的图示法，将力的三要素——大小、方向、作用点分别用线段的长短（结合标度）、箭头的指向、箭尾表示。
在这里提醒注意：物理量有两类，矢量和标量。矢量有大小和方向，标量只有大小而无方向。不过，这两类物理量最主要的区别是它们的运算法则，标量的运算法则是代数加减法，而矢量的运算法则是平行四边形定则。力的矢量性是力概念的一大难点。
4、力的分类
(1)按性质分，可分为重力（万有引力）、弹力、摩擦力、分子力、电磁力等。
(2)按效果分，可分为压力、支持力、动力、阻力、向心力、回复力等。
(3)按作用方式分，可分为场力和接触力。万有引力(重力)、电磁力均属于场力，弹力、摩擦力均属于接触力。
(4)按研究对象分，可分为外力和内力。
（二）重力
1、产生原因：由于地球的吸引而使物体受到的力。但它不等同于万有引力，它只是万有引力的一个分力，另一个分力提供物体随地球自转所需的向心力，在两极处重力等于万有引力。由于重力远大于向心力，一般情况下近似认为重力等于万有引力。
2、重力的方向：总是竖直向下（是指和水平面垂直的方向，除了在赤道和极地附近一般不是指向地心）
3、重力的大小：G＝mg
4、重力的作用点——重心：重力的等效作用点。重心的位置与物体的形状及质量的分布有关。重心不一定在物体上。质量分布均匀、形状规则的物体，重心在几何中心上．薄板类物体的重心可用悬挂法确定。
（三）弹力
1、弹力的产生条件：弹力的产生必须同时满足两个条件：（1）两个物体直接接触（2）发生弹性形变。
2、弹力的方向：和物体形变的方向相反，或者说和使物体发生形变的外力方向相反。
在实际问题中一般可以分三种情况来判断：（1）压力、支持力的方向总是垂直于接触面。若接触面是曲面则垂直于该处的切面。（2）绳对物体的拉力总是沿着绳收缩的方向。⑶杆对物体的弹力不一定沿杆的方向。如果轻直杆只有两个端点受力而处于平衡状态，则轻杆两端对物体的弹力的方向一定沿杆的方向。
3．弹力的大小：
对于弹簧，弹力的大小可以由胡克定律计算。对一般物体，如桌面、绳子等物体，弹力大小由物体的受力情况和运动情况共同决定。
胡克定律可表示为（在弹性限度内）：F=kx，还可以表示成ΔF=kΔx，即弹簧弹力的改变量和弹簧形变量的改变量成正比。
（四）摩擦力
1．摩擦力产生条件：摩擦力的产生必须同时符合四个条件：（1）两物体直接接触；（2）相互挤压；（3）接触面粗糙；（4）有相对运动或相对运动的趋势。这四个条件缺一不可。
2．滑动摩擦力大小：F=μFN，其中的FN表示正压力。特别注意：FN不一定等于重力G。
3．静摩擦力大小：对于静摩擦力，其大小不能用滑动摩擦定律F=μFN计算（在粗略计算或题目有要求时可认为其最大值等于滑动摩擦力，即Fm=μFN），一般要根据物体的受力情况和运动情况共同确定，其可能的取值范围是0＜Ff≤Fm。
4．摩擦力方向：摩擦力方向和物体间相对运动（或相对运动趋势）的方向相反。
特别注意的是“相对”二字。其实摩擦力的方向和物体的运动方向可能成任意角度。通常情况下摩擦力方向可能和物体运动方向相同（作为动力），可能和物体运动方向相反（作为阻力），可能和物体速度方向垂直（作为匀速圆周运动的向心力）。
（五）合力与分力：如果一个力产生的效果跟几个力共同作用所产生的效果相同，这个力就叫做那几个力的合力，那几个力叫做这个力的分力。
（六）力的合成与分解：求几个力的合力叫做力的合成；求一个力的分力叫做力的分解。
（七）力的合成
1、同一直线上两个力的合成：同方向时F=F1＋F2；反方向F=F1－F2
2、互成角度两力合成：遵从平行四边形法则
平行四边形法则：两个互成角度的力F1、F2的合成，可以把F1、F2的线段作为邻边作平行四边形，它的对角线即表示合力的大小和方向（如图1所示）。
平行四边形法则可简化为三角形定则，如图2：把F1、F2、矢量首尾相接画出来，把F1和F2的另外两端连接起来，则此连线就表示合力F的大小和方向。
通过分析可知，合力的取值范围是：| F1－F2|≤F≤F1＋F2
3、多力合成：可用平行四边形法则两个、两个地依次合成。
另外可用三角形定则。如求F1、F2、F3、…、Fn的合力,可以把F1、F2、F3、…、Fn等n个矢量首尾相接画出来，把F1和Fn的另外两端连接起来，则此连线就表示合力F的大小和方向.
（八）力的分解
1、力的分解遵循平行四边形法则，力的分解相当于已知对角线求邻边。
2、两个力的合力唯一确定，一个力的两个分力在无附加条件时，从理论上讲可分解为无数组分力，但在具体问题中，应根据力实际产生的效果来分解。
3、几种有条件的力的分解
（1）已知两个分力的方向，求两个分力的大小时，有唯一解。
（2）已知一个分力的大小和方向，求另一个分力的大小和方向时，有唯一解。
（3）已知两个分力的大小，求两个分力的方向时，其分解不惟一。
（4）已知一个分力的大小和另一个分力的方向，求这个分力的方向和另一个分力的大小时，其分解方法可能惟一，也可能不惟一。
4、正交分解法：把一个力分解成两个互相垂直的分力，这种分解方法称为正交分解法。
正交分解法的步骤：
①首先建立平面直角坐标系，并确定正方向
②把各个力向x轴、y轴上投影，但应注意的是：与确定的正方向相同的力为正，与确定的正方向相反的为负，这样，就用正、负号表示了被正交分解的力的分力的方向
显而易见，正交分解法也可以求合力，最易求的是各分力在x轴上的的代数和Fx合和在y轴上的代数和Fy合，进一步可以求所有力的合力，大小为：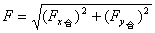
，
方向为：tanα=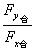
（α为合力F与x轴的夹角）
其实正交分解中的“分解”往往是为了“合成”。
解析：
根据平行四边形法则，作出示意图10，它是一个菱形，我们可以利用其对角线垂直平分，通过解其中的直角三角形求合力．
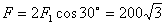N=346 N
合力与F1、F2的夹角均为30°．
点评：
对于求矢量，一定从矢量的特点出发，注意不仅要求出其大小，还要求出其方向，这才是完整的。而矢量的方向通常用它与已知方向的夹角来表示。
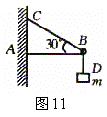
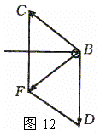
例7、水平横粱的一端A插在墙壁内，另一端装有一小滑轮B，一轻绳的一端C固定于墙上，另一端跨过滑轮后悬挂一质量m=10 kg的重物，∠CBA＝30°，如图11所示，则滑轮受到绳子的作用力为（g=10m/s2）
A．50N B．50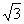
N C．100N D．100
N
解析：
取小滑轮作为研究对象，悬挂重物的绳中的弹力是T＝mg，故小滑轮受绳的作用力沿BC、BD方向的大小都是100N，分析受力如图12所示．其中∠CBD＝120°，∠CBF＝∠DBF，∴∠CBF=60°，∠CBF是等边三角形．故F＝100 N。
故C选项正确。
点评：
当两个物体间存在着多个力的作用时，要正确理解他们之间的作用力应该是这多个作用力的合力。
例8、如图13所示，质量为m的木块在推力F作用下，在水平地面上做匀速运动．已知木块与地面间的动摩擦因数为μ，那么木块受到的滑动摩擦力为
.