高考在选择题上主要考查等比数列的性质,解答题一般是难度较大的综合题,而更多地是在函数、不等式、数列、解析几何多种知识的网络交汇点处命题.应该注意这种命题趋势.
1、(湖南)已知数列{an}是首项为a且公比q不等于1的等比数列,Sn是其前n项和,a1,2a7,3a4成等差数列.
(Ⅰ)证明:12S3,S6,S12-S6成等比数列;
(Ⅱ)求和:Tn=a1+2a4+3a7+…+na3n-2.
本小题主要考查等差、等比数列的概念和基本性质,推理和运算能力.
解:(Ⅰ)证明由 成等差数列,得
成等差数列,得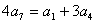 ,
,
即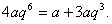 变形得
变形得
所以 (舍去).
(舍去).
由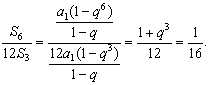

得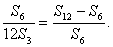 所以12S3,S6,S12-S6成等比数列.
所以12S3,S6,S12-S6成等比数列.
(Ⅱ)解: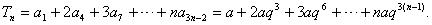
即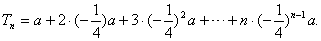 ①
①
①× 得:
得: ②
②
①-②有: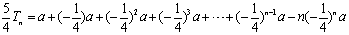
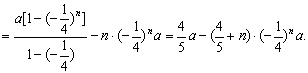
所以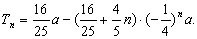
2、(全国高考题)
(1)已知数列{cn},其中cn=2n+3n,且数列{cn+1-pcn}为等比数列,求常数p;
(2)设{an}、{bn}是公比不相等的两个等比数列,cn=an+bn,证明数列{cn}不是等比数列.
本小题主要考查等比数列的概念和基本性质,推理和运算能力.
解:(1)因为{cn+1-pcn}是等比数列,故有:
(cn+1-pcn)2=(cn+2-pcn+1)(cn-pcn-1).
将 cn=2n+3n代入上式,得
[2n+1+3n+1-p(2n+3n)]2=[2n+2+3n+2-P(2n+1+3n+1)]·[2n+3n-p(2n-1+3n-1)]
即 [(2-p)2n+(3-p)3n]2=[(2-p)2n+1+(3-p)3n+1][(2-p)2n-1+(3-p)3n-1],
整理得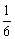 (2-p)(3-p)·2n·3n=0,
(2-p)(3-p)·2n·3n=0,
解得p=2或p=3.
(2)设{an}、{bn}的公比分别为p、q,p≠q,cn=an+bn.
为证{cn}不是等比数列只需证c22≠c1·c3.
事实上,c22=(a1p+b1q)2=a12p2+b12q2+2a1b1pq,
c1·c3=(a1+b1)(a1p2+b1q2)=a12p2+b12p2+a1b1(p2+q2).
由于p≠q,p2+q2>2pq,又a1、b1不为零.
因为c22≠c1·c3,故{cn}不是等比数列.
说明:
本题的(1)仅考察n=1,2,3的情况而得p的值不行,这样p的值不能保证对任意自然数n,cn+1-pcn,cn+2-pcn+1,cn+3-pcn+2成等比数列,学生熟悉证明数列是等比数列而不熟悉证明数列不是等比数列的问题,所以(2)的得分率不高.由于只要c1,c2,c3不成等比数列,则数列{cn}不是等比数列,只要证明c1,c2,c3不成等比数列,这样证明较为简单.本题的(2)也可用反证法,假设c22=c1c3,得出p=q,与题设矛盾,而证得本题.本题构题新颖,背景公平,没有现成的题型可以套用,能真正考查考生的数学能力,是一道优秀的试题.
3、(全国高考题)设{an}是由正数组成的等比数列,Sn是其前n项和,证明:
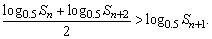
本题主要考查等比数列、对数、不等式等基础知识以及逻辑推理能力.
解:证法一:
设{an}的公比为q,由题设知a1>0,q>0.
(1)当q=1时,Sn=na1,从而

证法二:
设{an}的公比为q,由题设知a1>0,q>0.

(以下同证法1)
说明:
本试题将数列、对数函数和不等式综合在一起,全面考查了综合应用能力和分析解决问题的能力.
经分析知,要证出原不等式,只要证不等式Sn·Sn+2<Sn+12,上面的解法都是用的比较法.证法一中用求和公式,这时一定要分q≠1与q=1两种情况,q≠1时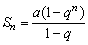 ,q=1时,Sn=na1.
,q=1时,Sn=na1.
证法二很巧妙地避免用求和公式,也就避免了讨论.证法一是通常的证法.高考重视对分类讨论方法的考查,每年试卷都有多道试题需分类讨论,应该掌握分类讨论的思想.