高考命题一般通过选择题、填空题来着重考查基本知识,基本技能,通过解答题着重对观察、归纳、抽象思维、逻辑推理以及灵活运用数学思想方法分析问题和解决问题能力进行考查,是历年高考的必考内容,其分值占总分的10%左右.
例1、(全国卷Ⅱ)如果a1,a2,…,a8为各项都大于零的等差数列,公差d≠0,则( )
A.a1a8>a4a5 B.a1a8<a4a5
C.a1+a8>a4+a5 D.a1a8=a4a5
分析:作差比较判别符号.a1a8-a4a5 =a1(a1+7d)-(a1+3d)(a1+4d)=-12d2<0,
∴a1a8<a4a5
答案:B
例2、(江苏卷)设无穷等差数列{an}的前n项和为Sn.
(I)若首项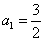 ,公差
,公差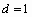 ,求满足
,求满足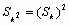 的正整数k;
的正整数k;
(II)求所有的无穷等差数列{an},使得对于一切正整数k都有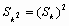 成立.
成立.
分析:本小题主要考查数列的基本知识,以及运用数学知识分析和解决问题的能力.
解:(I)当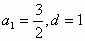 时,
时,
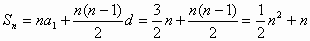
由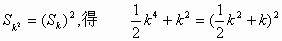 ,
,
即 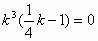 又
又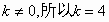 .
.
(II)设数列{an}的公差为d,则在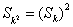 中分别取k=1,2,得
中分别取k=1,2,得
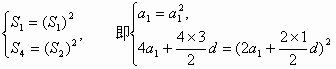
由(1)得 
当
若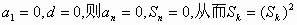 成立,
成立,
若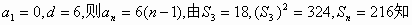
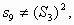
故所得数列不符合题意.
当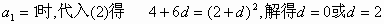
若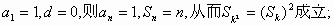
若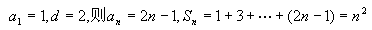
从而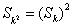 成立.
成立.
综上,共有3个满足条件的无穷等差数列:
①{an} : an=0,即0,0,0,…;
②{an} : an=1,即1,1,1,…;
③{an} : an=2n-1,即1,3,5,…,