指数、指数函数作为数学运算及基本函数在高考时往往与其它知识融合在一起被考查．
有关对数的知识在高考中往往与指数联系在一起，利用选择题或填空题的形式进行考查．主要考查指、对数的概念及性质．
例1、（1）（高考·全国卷III）若
则（ ）
A．a<b<c B．c<b<a
C．c<a<b D．b<a<c
（2）已知log2[log3(log4x)]=log3[log4(log2y)]=log4[log2(log3z)]=0，则x＋y＋z=（ ）
A．50 B．58
C．89 D．111
分析：
（1）这是一道利用对数的运算性质进行运算，进而判断数值大小的对数问题。
（2）利用1的对数是零，底的对数是1，从外到内分别求出x、y、z。
解：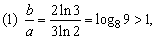
且a、b>0，∴b>a，
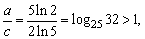且a、c>0，
∴a>c，∴b>a>c，故选C。
(2)由已知，log3(log4x)=1，∴log4x=3，∴x=43=64，
同理得y=16， z=9，故选C。
例2、（上海高考题）三个数60.7，0.76，log0.76的大小顺序是（ ）
A．0.76<log0.76<60.7 B．0.76<60.7<log0.76
C．log0.67<60.7<0.76 D．log0.76<0.76<60.7
分析：本题考查指数函数的性质与两个数大小的比较方法．
因0<0.76<1，60.7>1，log0.67<0，∴ log0.76<0.76<60.7.
答案：D
