对数的发现过程
16世纪的欧洲随着资本主义的迅速发展,科学和技术也一改中世纪停滞不前的局面.天文、航海、测绘、造船等行业不断向数学提出新的课题。有一个集中暴露出来令人头痛的问题是:在星体的轨道计算,船只的位置确定,大地的形貌测绘,船舶的结构设计等一系列课题中,人们所遇的数据越来越宠杂,所需的计算越来越繁难!无数的乘除、乘方、开方和其他运算,耗费了科学家们大量的极为宝贵的时间和精力。
面对这种局面,数学家们终于出来急其所难,各种门类的表格:平方表、立方表、平方根表、圆面积表等等,便应运而生,人类就这么在表格的海洋中茫然地行驶了半个多世纪,直到16世纪40年代,才迎来了希望的曙光。
公元1544年,著名的哥尼斯堡大学教授,德国数学家斯蒂费尔(stiefel,1487-1567),在简化大数计算方面迈出了重要的一步。在《普通算术》一书中,斯蒂费尔宣布自己发现了一种有关整数的奇妙性质,他认为:“为此,人们甚至可以写出整本整本的书……”
那么,斯蒂费尔究竟发现了什么呢?原来他如同下表比较了两种数列:等比数列和等差数列。
斯蒂费尔把等比数列的各数称为“原数”,而把等差数列的对应数称为“代表者”(即后来的“指数”)。他惊奇地发现:等比数列中的两数相乘,其乘积的“代表者”,刚好等于等差数列中相应两个“代表者”之和;而等比数列中的两数相除,其商的“代表者”,也恰等于等差数列中两个“代表者”之差。斯蒂费得出的结论是:可以通过如同上面那样的比较,把乘除运算化为加减运算!
可以说斯蒂费尔已经走到了一个重大发现的边缘。因为他所说的“代表者”y,实际上就是现在以2为底x的对数
y=log2x
而使斯蒂费尔惊喜万分的整数性质就是:
log2(M·N)=log2M+log2N
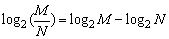
历史常常惊人地重复着这样的人和事:当发现已经降临到眼皮底下,只缘一念之差,却被轻轻错过!斯蒂费尔大约就是其中令人惋惜的一个。他困惑于自己的表格为什么可以算出16×256=4096,却算不出更简单的16×250=4000。他终于没能看出在离散中隐含着的连续,而是感叹于自己研究问题的“狭窄”。从而在伟大的发现面前,把脚缩了回去!
正当斯蒂费尔感慨于自己智穷力竭之际,在苏格兰的爱丁堡诞生了一位杰出人物,此人就是对数的发明人纳白尔(Napier,1550-1617)。
纳白尔出身于贵族家庭,天资聪慧,才思敏捷,从小又受家庭的良好熏陶,十三岁便进入了圣安德鲁斯大学的一个学院学习。十六岁出国留学,学识因之大进。公元1571年,纳白尔抱志回国。先是从事于天文、机械和数学的研究,并深为复杂的计算所苦恼。公元1590年,纳白尔改弦更张,潜心于简化计算的工作。他匠心独运,终于在斯蒂费尔的足迹上,向前迈出了具有划时代意义的一步!
说来也简单!纳白尔只不过是让任何数都找到了与它对应的“代表者”。这相当于在斯蒂费尔离散的表中,密密麻麻地插进了许多的中间值,使人看去宛如无数的纬线穿行于经线之中,显示出布匹般的连续!
公元1594年,纳白尔开始精心编制可供实用的对数表。在经历了7300个日日夜夜之后,一本厚达200页的八位数表终于诞生了!公元1614年,纳白尔发表了《关于奇妙的对数法则的说明》一书,书中论述了对数的性质,给出了有关对数表的使用规则和实例。纳白尔终于用自己20年的计算,换来了人世间无数寿命的延续!法国大数学家拉普拉斯说得好:“如果一个人的生命是拿他的一生中的工作多少来衡量,那么对数的发明,等于延长了人类的寿命!”
不幸的是,纳白尔的工作虽然延长了他人的寿命,却没能使自己的生命得以延长。就在纳白尔著作发表后的第三个年头,公元1617年,这位永受后人缅怀的杰出数学家,终因劳累过度,不幸谢世。
纳白尔的对数发明颇具传奇性。当时的欧洲,代数学仍处于十分落后的状态,甚至连指数概念尚未建立。在这种情况下先提出对数概念,不能不说是一种奇迹!纳白尔的对数是从一个物理上的有趣例子引入的:两个质点A、B有相同的初速度v。质点A在线段OR上作变速运动,其速度与它到R的距离成正比;质点B作匀速直线运动。今设AR=X,O′B=y,试求X,y之间的关系?
纳白尔经过仔细分析后发现;质点A的瞬时末速度是一个无穷递缩等比数列
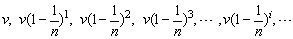
从而量x在变化时也可以看成是一个无穷递缩等比数列;而Y在变化时显然可以看成是一个无穷递增的等差数列
0, v,2v,3v,4v,…,tv,…
这样一来,在变量y与变量x之间例建立起了函数关系。纳白尔把y称为x的对数,用现在的式子来写就是:
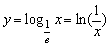
这里符号“ln”表示“自然对数”,对数的底就是常数e。这与今天课本上讲的“常用对数”有所不同,后者是以10为底的。
在数学上,对数函数的一般表示式为
y=logax
改写成指数形式便有
x=ay
在上式中,如果把变量x看成变量y的函数,并改用常用的函数和自变量符号,则有
y=ax
这样得到的函数,我们称为原函数的反函数。两个互为反函数的图象,在同一坐标系里,关于第Ⅰ、Ⅲ象限的角平分线为轴对称。反函数图象的这一特性,在上图中可以看得很明显。
对数是十七世纪人类最重大的发现之一。在数学史上,纳白尔的对数、笛卡儿的解析几何及牛顿莱布尼兹的微积分三者齐名,被誉为“历史上最重要的数学方法”!
对数于1653年传入我国。公元1664年,我国学者薛风祚(?-1680)编译了《天学会通》丛书。在国内,这是第一部介绍对数和对数表的著作。