对数函数是高考重点考查的知识之一,常常用选择题或填空题考查对数的基本概念和性质,也常在解答题中考查对数函数的性质的综合运用.
例1、(武汉模拟题)设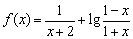 .
.
(1)判断f(x)的单调性,并给出证明;
(2)若f(x)的反函数为f-1(x),证明方程f-1(x)=0有惟一解;
(3)解关于x的不等式 .
.
解:


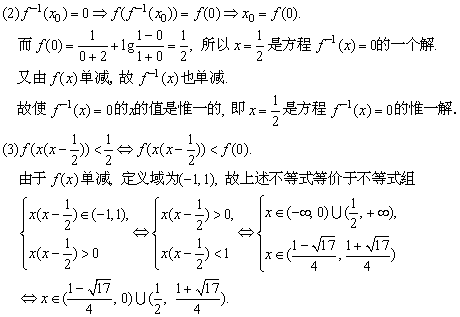
例2、(全国试题)使log2(-x)<x+1成立的x的取值范围是_________.
分析:本题考查对数函数和一次函数图象,图象的对称变换,以及数形结合的思想方法.
解答:作出y=log2(-x)及y=x+1的图象,由数形结合的思想方法知-1<x<0.
例3、设函数f(x)=|lgx|,若0<a<b,且f(a)>f(b),证明ab<1.
分析:若0<a<b<1,f(x)在(0,1)上递减,f(a)>f(b),此时ab<1.
若0<a<1,b>1,∵ f(b)-f(a)<0.
∴ lgb+lga<0,此时ab<1.
故ab<1.
证明:略.