三角函数的恒等变形是高考对三角部分考查的重点.高考对三角函数式恒等变形的考查体现了数学大纲对运算能力、逻辑推理能力的要求,同时注意对数学思想方法的考查.
试题多以计算为主,但在计算中应重视推理,掌握一些变形的技巧.在三角函数式的恒等变形中要注意角的变换和函数变换.角的变换指化为同角或凑特殊角.函数变换指化为同名函数,或化为正、余弦函数.
例1、(全国Ⅱ)设 为第四象限的角,若
为第四象限的角,若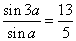 ,则
,则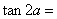 _____________.
_____________.
解析:
sin3α=3sinα-4sin3α,由已知得3-4sin2α=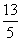 ,
,
∵α为第四象限角,∴sinα=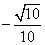 ,cosα=
,cosα=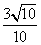 ,tanα=
,tanα= ,
,
∴tan2α=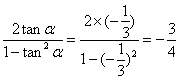 .
.
点评:
本题考查三角函数式的恒等变形及运算能力.上面解法的关键有两步,第一步依据和角公式将sin3α化为单角求出tanα;第二步利用倍角公式求tan2α.
例2、(天津高考题)已知 ,求
,求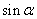 及
及 .
.
分析:
本题以三角函数的求值问题考查三角变换能力和运算能力,可从已知角和所求角的内在联系(均含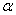 )进行转换得到.
)进行转换得到.
解法一:由题设条件,应用两角差的正弦公式得
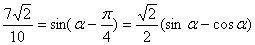 ,即
,即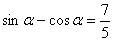 ①
①
由题设条件,应用二倍角余弦公式得
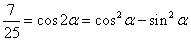
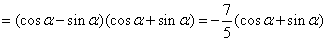
故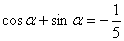 ②
②
由①和②式得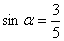 ,
,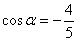

因此,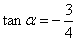 ,由两角和的正切公式
,由两角和的正切公式
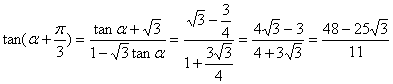 .
.
解法二:由题设条件,应用二倍角余弦公式得 ,
,
解得  ,即
,即

由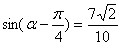 可得
可得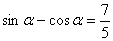

由于 ,且
,且 ,
,
故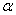 在第二象限于是
在第二象限于是 ,
,
从而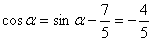

以下同解法一
点评:
在求三角函数值时,必须对各个公式间的变换应公式的条件要理解和掌握,注意隐含条件的使用,以防出现多解或漏解的情形.
例3、(全国高考题)已知△ABC的三个内角A、B、C,满足A+C=2B,
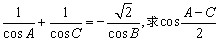 的值.
的值.
解法一:
由题设条件知B=60°,A+C=120°.
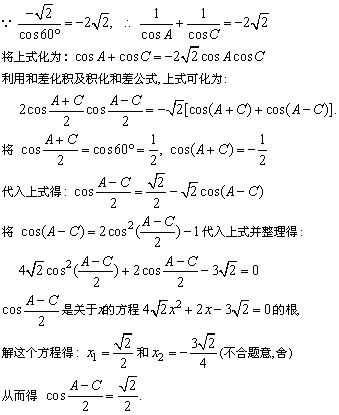
解法二:
由题设条件知B=60°,A+C=120°.


点评:
本题考查三角函数基础知识,利用三角公式进行恒等变形和运算的能力.需要用方程的思想解题,解的过程中把 当作未知数,设法得到关于
当作未知数,设法得到关于 的一元二次方程,就可求出
的一元二次方程,就可求出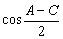 的值.
的值.