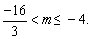例一、对任意实数λ,函数y=λ(x2-1)+x-a的图像与x轴恒有公共点,求实数a所应满足的条件.
精析:当λ≠0时,函数图象与x轴恒有公共点,
有方程λ(x2-1)+x-a=0恒有解,得△1≥0,
再由一元二次不等式成立,又有判断式△2≤0.
求得a所应满足的条件.
解答:原函数即为y=λx2+x-(λ+a),
当λ=0时,y=x-a为一次函数与x轴恒有公共点;
当λ≠0时,y=λx2+x-(λ+a)为二次函数,
要使其图象与x轴恒有公共点,
则△1=1+4λ(λ+a)=4λ2+4aλ+1≥0恒成立.
从而△2=(4a)2-4×4=16(a2-1)≤0,∴ -1≤a≤1.
∴实数a所满足的条件是:λ=0时,a∈R;λ≠0时,-1≤a≤1.
例二、假设国家收购某种农副产品的价格是120元/担,其中征税标准是每100元征税8元(叫做税率是8个百分点,即8%),计划可收购m万担,为了减轻农民负担,决定税率降低x个百分点,预计收购量可增加2x个百分点,要使此项税收在税率降低后不低于原计划的78%,试确定x的取值范围.
精析:此为应用题,关键是审好题,从中建立出数学模型进行求解.
解答:税率降低后是(8-x)%,收购量为m(1+2x%)万担,税收为120m(1+2x%)(8-x)%万元,原来的税收为120m·8%万元,根据题意可得
120m(1+2x%)(8-x)%≥120m·8%·78%,
即x2+42x-88≤0,解之-44≤x≤2,
又 x>0,∴ 0<x≤2,∴x 的取值范围是{x|0<x≤2}.
3、已知方程x2+2mx-m+12=0的两个实根都大于2,求实数m的取值范围.
精析:考虑对应的一元二次函数y=x2+2mx-m+12的图象,方程有这样的两个实数根等价于函数图像与x轴的两个交点的横坐标都大于2,结合图象特征及二次函数值的正、负,判别式等可得关于m的不等式组,从而求得m的范围.
解:设函数f(x)= x2+2mx-m+12,依条件得
得:
由此得: