函数与不等式是高中数学的重点内容,是高考的热点内容,而函数的定义域、值域,单调区间的求解,以及指数不等式、对数不等式、无理不等式等的求解,最终都化归为我们这里的几类基本不等式(组)的求解,其次高考中很多题都常常与它们有关,同时它们也有单独命题的时候,所以对这部分知识的掌握必须达到熟练的程度.
例一、(北京春招)若不等式|ax+2|<6的解集为(-1,2),则实数a等于()
A.8 B.2 C.-4 D.-8
解析:∵ |ax+2|<6, ∴-6<ax+2<6, -8<ax<4.
当a>0时,有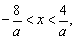 而已知原不等式的解集为(-1,2) 而已知原不等式的解集为(-1,2)
所以有 此方程无解(舍去). 此方程无解(舍去).
当a<0时,有 解得a=-4. 解得a=-4.
当a=0时,原不等式的解集为R,与题设不符(舍去),
故a=-4.
答案:C
例二、(全国)设a≠b,解关于x的不等式a2x+b2(1-x)≥[ax+b(1-x)]2.
解析:本题主要考查不等式的基本性质,一元二次不等式的解法及学生的运算能力.
不等式变形得(a-b)2(x2-x)≤0,
∵a≠b,∴(a-b)2>0,
∴x2-x≤0,解得解集为{x|0≤x≤1}.
例三、(上海)关于实数x的不等式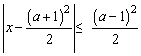 及x2-3(a+1)x+2(3a+1)≤0的解集依次记为A和B,求使 及x2-3(a+1)x+2(3a+1)≤0的解集依次记为A和B,求使 时a的取值范围. 时a的取值范围.
解析:本题考查含绝对值不等式,一元二次不等式的解法,子集等基本知识,考查学生分类讨论及运算能力.
由  , 得 , 得
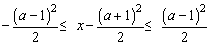
∴ 2a≤x≤a2+1,即A={x|2a≤x≤a2+1}.
由 x2-3(a+1)x+2(3a+1)≤0,
得 (x-2)[x-(3a+1)]≤0
(1)当3a+1≥2即a≥ 时,B={x|2≤x≤3a+1}, 时,B={x|2≤x≤3a+1},
要使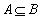 ,必需 ,必需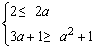 ,此时1≤a≤3. ,此时1≤a≤3.
(2)当3a+1<2,即a<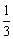 时,B={x|3a+1≤x≤2}, 时,B={x|3a+1≤x≤2},
要使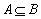 ,需 ,需 ,此时a=-1. ,此时a=-1.
综合知使 的a的取值范围是1≤a≤3,或a=-1. 的a的取值范围是1≤a≤3,或a=-1.
|