这一节的内容仍然在高考中经常出现,在这一节里要掌握函数图象的平移变换,伸缩变换,重点是掌握函数的图象与图象之间的关系,并能够根据函数图象写出三角函数表达式
例1、(全国高考试题)关于函数f(x)=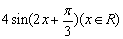 ,有下列命题:
,有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可改写成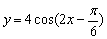 ;
;
③y=f(x)的图象关于点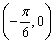 对称;
对称;
④y=f(x)的图象关于直线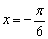 对称.
对称.
其中正确的命题序号为___________.
分析:逐一判断四个命题的真伪即可得解.
解答:
由于正弦曲线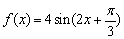 在每个周期
在每个周期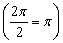 内两次经过x轴,
内两次经过x轴,
因此满足f(x1)=f(x2)=0的x1-x2未必是π的整数倍,故命题(1)不正确.
由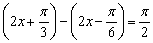 ,故
,故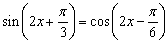 ,
,
即命题(2)正确.
由于正弦曲线f(x)与x轴的每个交点都是它的对称中心,
将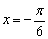 代入
代入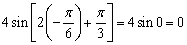 ,因此点
,因此点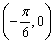 是f(x)的图象的一个对称中心,
是f(x)的图象的一个对称中心,
故命题(3)正确.
正弦曲线f(x)的对称轴必经过图象的最高点或最低点,且与y同平行,而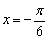 时y=0,点
时y=0,点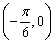 不是最高点也不是最低点,故直线
不是最高点也不是最低点,故直线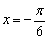 不是图象的对称轴,因此命题(4)不正确,综上所述,应该选(2)、(3).
不是图象的对称轴,因此命题(4)不正确,综上所述,应该选(2)、(3).
例2、(全国Ⅱ高考试题)函数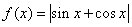 的最小正周期是( )
的最小正周期是( )
A.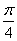 B.
B.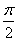 C.
C.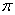 D.
D.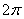
解析:
∵f(x)=|sinx+cosx|=| sin(x+
sin(x+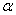 )|,∴T=
)|,∴T=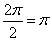 ,
,
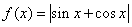 的最小正周期是π.选C.
的最小正周期是π.选C.
例3、(湖北高考试题)设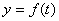 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中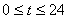 .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
t |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
y |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观察,函数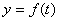 的图象可以近似地看成函数
的图象可以近似地看成函数 的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是( )
的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是( )
A.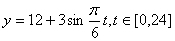 B.
B.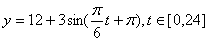
C.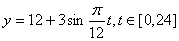 D.
D.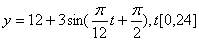
解析:观察得T=12,∴ω= ,排除C、D,令t=3,由y=15.1,可知选A.
,排除C、D,令t=3,由y=15.1,可知选A.