例1、是否存在满足0≤α＜β≤π 的实数α、β，使F（θ）=sin2θ+sin2(θ+α)+ sin2(θ+β)的值是不随θ变化的常数.

解：

　　整理得：，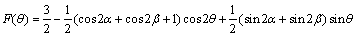

　　F（θ）为常数的充要条件是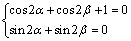：解得．

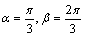　　所以满足0≤α＜β≤π的实数α、β存在.

例2、已知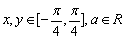，且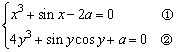

　　 试求cos(x＋2y)的值.

分析一：

　　由于已知条件中涉及到变量较多，而要求的式子中只含有x，y，故考虑将已知条件中的a消去.

解答：

　　由①＋②×2得x3＋(2y)3＋sinx＋sin2y=0

　　

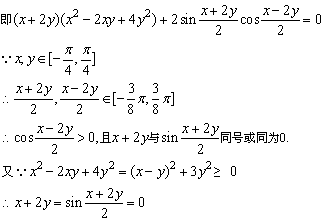
　　从而cos(x＋2y)=cos0=1.

分析二：

　　通过观察已知条件的特点，联想所学知识，可利用函数方程的观点来解决.

解答：

　　由已知条件变形得：

　　

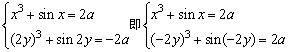
　　故x,－2y可看作方程t3＋sint=2a的两根.

　　令f(t)= t3＋sint,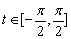，则f(t)为增函数，其图象与直线y=2a只有一个交点.

　　从而x=－2y，即x＋2y=0

　　∴cos(x＋2y)=1.

-END-