1、下列命题中正确的是( )
A.将y=sinx的图像沿x轴向右平移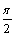 个单位,得到y=cosx的图像
个单位,得到y=cosx的图像
B.函数y=sin(x+φ)的图像,当φ>0时由y=sinx的图像向右平移φ个单位得到
C.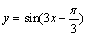 的图像可由
的图像可由 的图像上所有点的纵坐标不变,横坐标缩小为原来的
的图像上所有点的纵坐标不变,横坐标缩小为原来的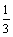 倍得到
倍得到
D.y=2sin3x的图像可由y=3sin3x的图像上各点横坐标不变,纵坐标缩小为原来的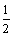 倍得到
倍得到
2、函数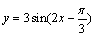 的图像可以由函数y=sin2x的图像经过下列哪种变换得到( )
的图像可以由函数y=sin2x的图像经过下列哪种变换得到( )
A.向右平移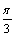 个单位 B.向右平移
个单位 B.向右平移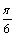 个单位
个单位
C.向左平移 个单位 D.向左平移
个单位 D.向左平移 个单位
个单位
3、在[-π,π]上既是增函数,又是奇函数的是( )
A.y=sin2(π-x) B.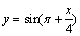
C.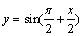 D.
D.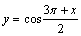
4、下图是周期为2π的三角函数y=f(x)的图像,那么f(x) 可以写成( )
A.sin(1+x) B.sin(-1-x)
C.sin(x-1) D.sin(1-x)
5、函数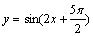 的图像的一条对称轴方程是( )
的图像的一条对称轴方程是( )
A. B.
B.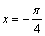
C.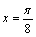 D.
D.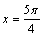
6、已知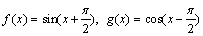 ,则f(x)的图像( )
,则f(x)的图像( )
A.与g(x)的图像相同
B.与g(x) 的图像关于y 轴对称
C.向左平移 个单位,得到g(x)的图像
个单位,得到g(x)的图像
D.向右平移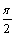 个单位,得到g(x)的图像
个单位,得到g(x)的图像
7、函数f(x)=cos(3x+φ)的图像关于原点中心对称的充要条件是( )
A. B.
B.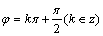
C.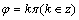 D.
D.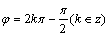
8、正弦函数y=f(x)的定义域为R,周期为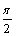 ,初相为
,初相为 ,值域为[-1,3],则其函数式的最简形式为( )
,值域为[-1,3],则其函数式的最简形式为( )
A. B.
B.
C.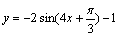 D.
D.
9、函数f(x)=2sinωx(ω﹥0)在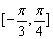 上递增,则( )
上递增,则( )
A.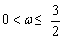 B.0﹤ω≤2
B.0﹤ω≤2
C.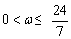 D.ω≥2
D.ω≥2
10、对于函数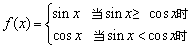 ,给出下列四个命题
,给出下列四个命题
①该函数的值域是[-1,1].
②当且仅当 时,该函数取得最大值.
时,该函数取得最大值.
③该函数是以π为周期的周期函数.
④当且仅当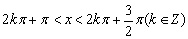 时,f(x)﹤0
时,f(x)﹤0
上述命题中正确的是( )
A.① B.②
C.③ D.④