1、已知集合P=[-4,4],Q=[-2,2],下列对应x→y,不表示从P到Q映射的是( )
A.2y=x B.y2= (x+4)
(x+4)
C.y=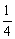 x2-2 D.y=-
x2-2 D.y=-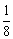 x2
x2
2、函数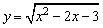 +log2(x+2)的定义域为( )
+log2(x+2)的定义域为( )
A.(-2,-1]∪[3,+∞) B.(-∞,-1)∪(3,+∞)
C.(-∞,-1]∪[3,+∞) D.(-2,-1]
3、函数y=f(2x)的定义域为[-1,1],则函数y=f(log2x)的定义域为( )
A.[-1,1] B.[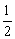 ,2]
,2]
C.[1,2] D.[ ,4]
,4]
4、函数f(x)=ax-1的反函数的图像经过点(4,2),则f-1(2)的值是( )
A.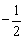 B.
B.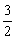
C.2 D.4
5、已知函数y=f(x)的图像与函数y=2-x-1的图像关于直线 y=x对称,则f(3)的值为( )
A.1 B.-1
C.-2 D.2
6、已知f(x)=log2(x+1),且a>b>c>0,则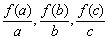 的大小关系是( )
的大小关系是( )
A.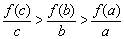 B.
B.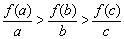
C.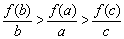 D.
D.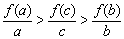
7、已知f(x)=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
A.[0,2] B.[1,2]
C.[1,+∞) D.(-∞,2]
8、若函数f(x)在R上是减函数,那么f(2x-x2)的单调递增区间是( )
A.(-∞,1] B.[-1,+∞)
C.(-∞,-1] D.[1,+∞)
9、某商品价格前两年每年平均递增20%,后两年每年平均递减20%,则四年后的价格与原来价格比较,变化情况是( )
A.增7.84% B.减7.84%
C.减9.5% D.不增不减
10、已知函数f(x)=3-2|x|,g(x)=x2-2x,构造函数F(x),定义如下:当f(x)≥g(x)时,F(x)=g(x),当f(x)<g(x)时,F(x)=f(x),那么F(x)( )
A.有最大值3,最小值-1
B.有最大值7-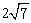 ,无最小值
,无最小值
C.有最大值3,无最小值
D.无最大值,也无最小值
11、已知函数f(x)=lg(ax-bx)(a>1>b>0),则不等式f(x)>0的解集为(1,+∞)的充要条件是( )
A.a=b+1 B.a<b+1
C.a>b+1 D.b=a+1
12、已知a>0且a≠1,f(x)=x2-ax,当x∈(-1,1)时,均有f(x)<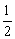 ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.(0,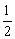 ]∪[2,+∞) B.[
]∪[2,+∞) B.[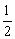 ,1)∪(1,2]
,1)∪(1,2]
C.(0,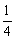 ]∪[4,+∞) D.[
]∪[4,+∞) D.[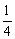 ,1)∪(1,4]
,1)∪(1,4]
[提示]
13、若函数f(x)=4x2-mx+5在区间[-2,+∞)上是增函数,则f(1)的最小值为_______.
14、函数y=lg(ax+1)的定义域为(-∞,1),则a的值是_______.
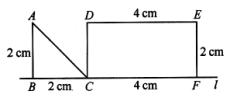
15、如图,直角边长为2cm的等腰直角三角形以2cm/s的速度自C点沿直线l匀速向右移动,则该三角形与矩形CDEF重合部分面积y(cm2)与时间t(s)的函数关系为y=_______(其中0≤t≤2).
16、设有两个命题,①不等式|x|+|x-1|>m的解集为R.②函数f(x)=-(7-3m)x是减函数.如果这两个命题中有且只有一个为真命题,则实数m的范围为_______.