设y=f(x)定义域为A，u=g(x)的定义域为B，则复合函数y=f[g(x)]在定义域{x|x∈B且g(x)∈A}上的单调性：
（1）当y=f(u)与u=g(x)的单调性相同时，y=f[g(x)]为增函数；
（2）当y=f(u)与u=g(x)的单调性相反时，y=f[g(x)]为减函数.
下面就y=f(u)、u=g(x)均为增函数来证明.
设x1、x2∈{x|x∈B且g(x)∈A}，且x1<x2.
∵ u=g(x)是增函数，∴ g(x1)<g(x2)，即u1<u2.
又∵ y=f(u)是增函数，∴ f(u1)<f(u2)，即f[g(x1)]<f[g(x2)].
∴ y=f[g(x)]为增函数，其余情况大家可类似作出证明.
例1、已知f(x)是（0，＋∞）上的减函数，则f(4－x2)的单调递减区间是（ ）
A、（0，＋∞） B、（－∞，0）
C、（0，2） D、（－2，0）
解：函数f(4－x2)的定义域为（－2，2），在（－2，0）上g(x)=4－x2为增函数.
∴ f(4－x2)的递减区间为（－2，0），选D.
答案：D
例2、已知y=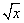
在（0，＋∞）上是增函数，如果
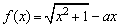（a>0）在[0，＋∞）上是减函数，求实数a的取值范围.
解：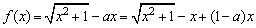
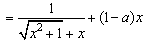
∵ y=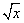
在[0，＋∞）上是增函数，且x2＋1在[0，＋∞）上是增函数，
∴ 
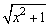在[0，＋∞）上是增函数，
∴ 
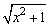＋x在[0，＋∞）上是增函数，
∴ 
在[0，＋∞）上是减函数．
若a≥1，则(1－a)x在[0，＋∞）上是减函数或常数函数.
∴ 当a≥1时，f(x)在[0，＋∞）上是减函数.
而当0<a<1，∵ f(0)=1，f(1)=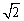
－a，f(0)与f(1)大小关系不定.
∴ f(x)在[0，＋∞）没有单调性.
综上，当a≥1时，f(x)在[0，＋∞）上是减函数.
例3、设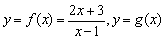
的图象与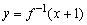
的图象关于y=x对称，求g(3)的值．
解析：由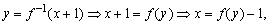
将x、y互换，
得y=f(x)-1应是y=f-1(x+1)的反函数，即g(x)=f(x)-1.
∴ 
．
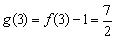评述：灵活运用反函数定义，显得轻盈活泼.
