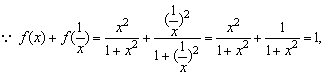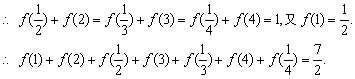函数是高中数学的重要内容，历年高考试题对函数内容的考查的比例较大．函数的概念及表示法是函数的基础，要求能准确、深刻地理解概念，灵活地加以运用.
例1、（北京）某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元.
（1）当一次订购量为多少个时，零件的实际出厂单价恰降为51元？
（2）设一次订购量为x个，零件的实际出厂单价为P元，写出函数P=f(x)的表达式.
（3）当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个，利润又是多少元？（工厂售出一个零件的利润=实际出厂单价－成本）
解答：
（1）设每个零件的实际出厂价恰好降为51元时，一次订购量为x0个，
则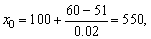
因此，当一次订购量为550个时，
每个零件的实际出厂价恰好降为51元.
（2）当0<x≤100时，P=60；当100<x<550时，P=60－0.02(x－100)=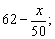
当x≥550时，P=51，
所以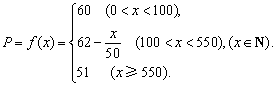
（3）设销售商的一次订购量为x个时，工厂获得的利润为L元，则
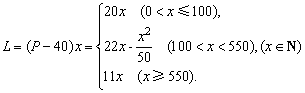
当x=500时，L=6000；当x=1000时，L=11000.
因此，当销售商一次订购500个零件时，该厂获得的利润是6000元；如果订购1000个，利润是11000元.
例2、（上海春招）对于函数f(x)，若存在x0∈R，使f(x0)=x0成立，则称x0为f(x)的不动点.已知函数f(x)=ax2＋(b＋1)x＋b－1(a≠0).
（1）当a=1, b=－2时，求函数f(x)的不动点.
（2）若对任意实数b，函数f(x)恒有两个相异的不动点，求a的取值范围.
（3）在（2）的条件下，若y=f(x)图像上A、B两点的横坐标是函数f(x)的不动点，且A、B两点关于直线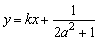
对称，求b的最小值.
分析：由题意不动点x0是满足f(x0)=x0的方程的根，理解好函数与方程之间的关系。
解答：
（1）a=1, b=－2时，f(x)=x2－x－3,
由题意可知x=x2－x－3，
得x1=－1,x2=3，故当a=1，b=－2时，f(x)的两个不动点为－1，3；
（2）∵f(x)=ax2＋(b＋1)x＋b－1(a≠0)恒有两个不动点，
∴x=ax2＋(b＋1)x＋b－1即ax2＋bx＋b－1=0恒有两个相异的实数根，得：
△=b2－4ab＋4a>0(b∈R)恒成立.解得0<a<1.
故当b∈R，f(x)恒有两个相异的不动点时，a的取值范围为0<a<1
（3）由题意，A、B两点应在直线y=x上，设A(x1, y1)，B(x2, y2)。
∵点A、B关于直线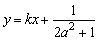
对称，∴k=－1.
设AB中点为M(x′,y′),
∵x1, x2是方程ax2＋bx＋b－1=0的两个根，
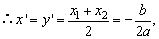于是，由M在直线
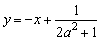上，
得
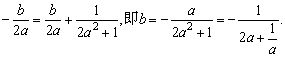
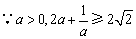，当且仅当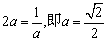
时取等号.
故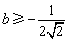
时，得b的最小值为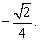
例3、（全国高考题）已知函数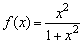
，那么
f(1)＋f(2)＋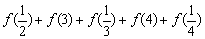
=______________.
分析：
已知函数解析式，可以把自变量的值代入求值，只是计算过于繁琐.若观察到自变量的特征，可以联想到f(x)＋f(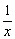
)的函数值特征.
解答：
