假设有两个函数：y=f(u)，u=g(x)，则函数y=f[g(x)]称为复合函数.
设函数y=f(u)的定义域为A，u=g(x)的定义域为B，则函数y=f[g(x)]的定义域为C={x|x∈B且g(x)∈A}.
例1、已知函数y=f(x)的定义域为[－1，2]，求下列函数的定义域.
（1）y=f(x－2x2)；
（2）y=f(x2)；
（3）y=f(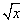
).
解答：
（1）函数y=f(x－2x2)是由函数y=f(u)与u=x－2x2复合而成，由y=f(u)的定义域为[－1，2]，u=x－2x2的定义域为R，由－1≤x－2x2≤2，解得－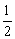
≤x≤1.
∴ 函数y=f(x－2x2)的定义域为[－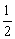
，1].
（2）同理，u=g(x)=x2的定义域为R，由－1≤x2≤2，解得︰－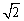
≤x≤2.
∴ y=f(x2)的定义域为[－
，
].
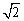（3）同理，u=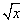
的定义域为[0，＋∞)，由－1≤
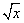≤2，得0≤x≤4，
∴ y=f(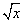
)的定义域为[0，4].
例2、已知函数y=f(x)的定义域为[0，＋∞），设函数g(x)=f(1－|x-a|)＋f(1－|x＋a|)(a>0)，试确定a的取值范围并求出函数g(x)的定义域.
解答：设f(1－|x－a|)的定义域为A，f(1－|x＋a|)的定义域为B.
则A=[－1＋a，1＋a]，B=[－1－a，1－a].
∵ a>0，∴ －1＋a>－1－a，1＋a>1－a.
且g(x)的定义域为A∩B≠
.
∴ 1－a≥－1＋a，∴ a≤1，又a>0，∴ 0<a≤1.
此即为a的取值范围.
当a=1时，1－a=－1＋a=0，此时A∩B={0},
当0<a<1时，1－a>－1＋a，此时A∩B=[－1＋a，1－a]
∴ 当a=1时，g(x)的定义域为{0}
当0<a<1时，g(x)的定义域为[－1＋a，1－a].
