“数学是锻炼思维的体操”.思维是大脑对事物的性质、它们之间的关系的认识过程.因为客观事物不是孤立存在的,是互相关联、互相影响的,往往具有某种因果关系,所以思维使我们能够知道并没有直接感觉到的事物,预见事情的进程和发展结果.就是从一些已知事实,推断出一些合理的结论.
正确的思维,应该是确定的,首尾一贯的,无矛盾的和有根据的.“逻辑”就是思维的规律.本讲讨论的“逻辑问题”,主要是判断推理问题.
例1、现有红、黄、蓝、白、紫五种颜色的珠子各一颗,用纸包着,在桌子上排成一行,由甲、乙、丙、丁、戊五人,猜各包内珠子的颜色,每人只许猜两包.
甲猜:第二包是紫的,第三包是黄的;
乙猜:第二包是蓝的,第四包是红的;
丙猜:第一包是红的,第五包是白的;
丁猜:第三包是蓝的,第四包是白的;
戊猜:第二包是黄的,第五包是紫的.
事后,打开纸包,发现每人都只猜对了一包,并且每包都只有一人猜对.问他们各猜对的是哪一种颜色的珠子.
解:根据题意我们列一个表:
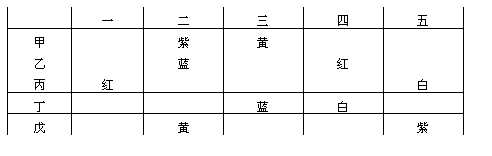
因为每包都只有一人猜对,第一包只有丙猜,所以丙猜第一包是红的猜对了.又因为每人只猜对一包,因此页第五包猜错了;而第五包由丙、戊两人猜,戊猜对了第五包是紫的.
由于第一包是红的,第四包只能是白的,因此,丁猜对了第四包,甲猜对了第三包.
甲、戊都猜错了第二包,只有乙猜对了第二包是蓝的.综上所述,甲猜对了第三包是黄的,乙猜对了第二包是蓝的,丙猜对了第一包是红的,丁猜对了第四包是白的,戊猜对了第五包是紫的.
说明:
由于第一包只有一人猜,一定是猜对了.因此,确定第一包的颜色,是解决这道题的突破口.解决问题,找到突破口是很重要的.用“列表方法”把繁杂的条件更加条理化,是解决“罗辑问题”的有效手段.
例2、刘毅、马明、张健三个男同学都各有一个妹妹,六人在一起举行乒乓球混合双打练习.规定兄妹不许搭伴.第一盘是刘毅和小萍对张健和小英;第二盘是张健和小红对刘毅和马明的妹妹.推断刘毅、马明、张健的妹妹各是谁?
解:先列表分析,非兄妹关系画“×,兄妹关系画“√”,暂不能肯定画“?”.

由表中可看出张健的妹妹是小萍.刘毅、马明的妹妹分别是谁只有两种可能:
第一,刘毅的妹妹是小英,马明的妹妹是小红.第二,刘毅的妹妹是小红,马明的妹妹是小英.
对第一种可能,第二盘练习就是张健和小红对刘毅和小红(马明的妹妹).不合理.对第二种可能,第二盘练习就是张健和小红对刘毅和小英.合理.
综合以上推断,刘毅的妹妹是小红,马明的妹妹是小英,张健的妹妹是小萍.
说明:
本题推断过程中,对可能的两种情况,进行-一检验,排除不合理的情况,肯定合理的情况.这是采用了“穷举法”.下面我们用穷举法再讨论一道题.
例3、王红、李智、张慧三名同学中,有一人在教室没其他同学的时候,把教室打扫得干干净净.事后,老师问他们三人,是谁做的好事.王红说:“是李智干的”;李智说:“不是我干的”;张慧也说:“不是我干的”.后来知道他们三人中,有两人说的是假话,有一人说的是真话.你能断定教室是谁打扫的吗?
解:由题意知只有三种可能,
如果是王红干的,那么王红说的“是李智干的”是假话;李智说的“不是我干的”是真话;张慧说的“不是我干的”也是真话.不符合题意中“两假一真”条件.
如果是李智干的,那么王红说的“是李智干的”是真话;李智说的“不是我干的”是假话;张慧说的“不是我干的”是真话.也不符合“两假一真”条件.
只能是张慧干的.这样王红、张慧说的是假话,李智说的是真话.符合“两假一真”.
例4、A、B、C、D、E五个球队进行单循环赛(每两个队之间都要比赛一场),进行到中途,发现A、B、C、D、比赛过的场次分别是4,3,2,1.问这时E队赛过几场?E队和哪个队赛过?
解:
解法一 用图表示各队之间是否比赛过.用平面上的点表示A、B、C、D、E队,两队比赛过,用两点连线表示,没有比赛过,则不连线.
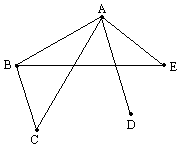
A赛过4场,A与B、C、D、E均连线;B赛过三场,除与A赛过,还赛过2场,因为D只赛过1场(和A队赛),因此B只能和C、E赛过;这样正好符合C赛过2场,D赛过1场.由图看出这时E队赛过2场,E队和A、B队赛过.
解法二 因为比赛一场,双方各计一次,因此,比赛过程中任何阶段,各队比赛的场次数总是偶数.A,B,C,D的场次数之和是4+3+2+1=10,是偶数,这时E赛过场次数一定也是偶数,有三种可能:0,2,4,因为A赛过4场,一定和E赛过.E不可能赛0场;又D只赛过一场,和A赛过,还没和E赛过,E不会赛过4场.只能是赛过2场.E和A赛过,B赛过3场,而B和D没赛过,B一定和E赛过.
综合以上分析,E赛过2场,E和A、B各赛一场.
说明:
用图表示所研究对象及其关系,是讨论逻辑问题的又一个重要手段.用点表示所研究对象,用连线表示对象之间的某种关系.充分利用图形的直观性,便于说明问题.
例5 老师要从甲、乙、丙、丁四名同学中选派两人去参加某项活动,征求他们的意见,甲说:“我服从分配”;乙说:“如果甲去,那么我就去”;丙说:“如果我不去,那么乙也不能去”;丁说:“我和甲,要去都去,要不去就都不去”.老师要都满足他们的要求,应选派谁去?
分析:
我们把命题“如果具有条件A,那么就有结论B,”表示成:ATB,符号“T”读作“推出”.根据题意老师应满足的条件是:
甲T乙(乙说),非丙T非乙,(丙说)这句话相当于乙T丙,甲?丁(丁说).把这些关系联系起来,很容易得出结论.
解:题目所要求的条件如下: