例1、(全国)设A,B,I均为非空集合,且满足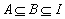 ,则下列各式中错误的是( )
,则下列各式中错误的是( )
A.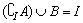 B.
B.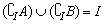
C.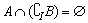 D.
D.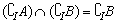
分析:
本题借助韦恩图举反例,易判断结论B错误.当且仅当A=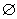 时,结论B正确,如图,可知
时,结论B正确,如图,可知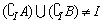 .
.
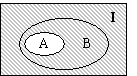
答案:B
例2、已知全集U={|a-1|,(a-2)(a-1),4,6}.
(1)若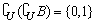 ,求实数a的值;
,求实数a的值;
(2)若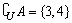 ,求实数a的值.
,求实数a的值.
分析:
本题主要考查集合的基本性质,集合的基本运算及分析问题解决问题的能力.
解答:
(1)∵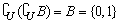 ,且B
,且B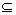 U,
U,
∴|a-1|=0,(a-2)(a-1)=1,或|a-1|=1,(a-2)(a-1)=0,
第一种情况显然不可能.在第二种情况中,由|a-1|=1得a=0,或a=2,
∴a=2适合. a的值为2.
(2)依题意知|a-1|=3或(a-2)(a-1)=3,若|a-1|=3,则a=4或a=-2;
若(a-2)(a-1)=3,则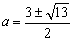 ,经检验知a=4时,(4-2)(4-1)=6,
,经检验知a=4时,(4-2)(4-1)=6,
与元素的互异性矛盾,∴所求a的值是-2或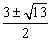 .
.
例3、(上海高考试题)设集合A=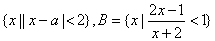 ,若A
,若A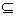 B,求实数a的取值范围.
B,求实数a的取值范围.
分析:
本题是一道研究集合和包含关系与解不等式相结合的综合性题目.主要考查集合的概念及运算,解绝对值不等式、分式不等式和不等式组的基本方法.在解题过程中要注意利用不等式的解集在数轴上的表示方法.体现了数形结合的思想方法.
解答:
由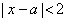 得,
得,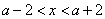 ,所以
,所以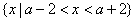 .由
.由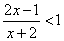 得
得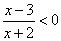 ,即
,即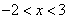 ,所以B=
,所以B=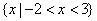 .因为A
.因为A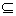 B,所以
B,所以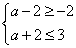 ,于是
,于是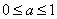 .
.