1、（上海）设a1、b1、c1、a2、b2、c2、均为非零实数，不等式a1x2＋b1x＋c1>0和a2x2＋b2x＋c2>0的解集分别为集合M和N，那么“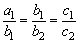
”是“M=N”的什么条件？
分析：利用二次函数与一元二次不等式的关系.
∵如果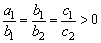
，则“M=N”，
如果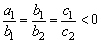
则“M≠N”，
∴“
”
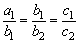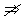“M=N”；
反之若M=N=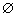
，即说明二次不等式的解集为空集，与它们的系数比无任何关系，只要求判别式小于零．因此，“M=N”
“
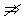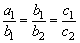”，因此既非充分也非必要条件．
答案：即非充分又非必要条件
2、（高考试题）设a,b是两个实数，集合A={(x,y)|x=n,y=na＋b,n∈Z},B={(x,y)|x=m,y=3m2＋15,m∈Z},C={(x,y)|x2＋y2≤144}是xoy平面内的点集，讨论是否存在a与b，使是A∩B≠
和(a,b)∈C同时成立？
分析：解决此题的关键是集合语言向非集合数学语言转化，将隐晦的数学含义显露出来．
解法：
假设存在实数a与b，同时满足题设中的两个条件，即有：
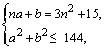从中消去b得a2＋(3n2＋15－na)2≤144,
即： (1＋n2)a2－2n(3n2＋15)a＋(3n2＋15)2－144≤0.
此时判别式△=4n2(3n2＋15)2－4(1＋n2)[(3n2＋15)2－144]
=36(－n4＋6n2－9）
=－36(n2－3)2
∵n∈Z,∴△<0,又二次项系数1＋n2>0,
∴上述关于a的二次不等式无解，因此同时满足题意中两个条件的实数a与b是不存在的.
