1、在数列0,3,8,x,24,35,48中,x应等于( )
A.11 B.12
C.15 D.17
2、已知数列-1,a1,a2,-4成等差数列,-1,b1,b2,b3,-4成等比数列,则 的值是( )
的值是( )
A.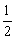 B.
B.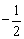
C.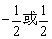 D.
D.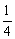
3、等差数列{an}中,已知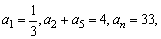 则n为( )
则n为( )
A.48 B.49
C.50 D.51
4、设a1=2,an+1=2an+3,则通项an可能是( )
A.5-3n B.3×2n-1-1
C.5-3n2 D.5×2n-1-3
5、在等差数列中,已知a1+a4+a7=45, a2+a5+a8=39,则a3+a6+a9的值是( )
A.33 B.30
C.27 D.24
6、已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<logm(ab)<1,则m的取值范围是( )
A.(0,1) B.(1,+∞)
C.(0,8) D.(8,+∞)
7、等差数列中a1+3a8+a15=120,则2a9-a10的值是( )
A.24 B.22
C.20 D.-8
8、已知{an}是等差数列,其前n项和为Sn,若S9=18,Sn=240,an-4=30,则n的值是( )
A.10 B.12
C.15 D.18
9、已知条件甲为“三数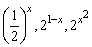 成等比数列”,条件乙为“lgx,lg(x+1), lg(x+3)成等差数列”,则甲是乙成立的( )
成等比数列”,条件乙为“lgx,lg(x+1), lg(x+3)成等差数列”,则甲是乙成立的( )
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分又不必要条件
10、设{an}是由正数组成的等比数列,公比q=2,且a1a2a3…a30=230,那么a3a6a9…a30等于( )
A.230 B.220
C.240 D.260
11、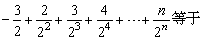 ( )
( )

12、已知数列{an}满足an+1=an-an-1 (n≥2), a1=a, a2=b,Sn=a1+a2+…+an,则下列结论正确的是( )
A.a100=-a, S100=2b-a
B.a100=-b, S100=2b-a
C.a100=-b, S100=b-a
D.a100=-a, S100=b-a
13、已知数列的通项公式an=n2-4n-12(n∈N*),这个数列从第_______项起各项为正数.
14、在等比数列{an}中,Sn=a1+a2+…+an,已知a3=2S2+1,a4=2S3+1,则公比q=_____.
15、等差数列{an}中,a1>0,前n项和为Sn,且S9>0, S10<0,则n=______时,Sn最大.
16、在等比数列{an}中,已知a2=6,且a5-2a4-a3+12=0,则an=______.