求数列的和与通项公式在高考题型中较为常见，已知Sn与an的关系求Sn或an的问题在试题中经常出现．对于由递推关系式给出的数列，了解由它求通项的方法很有必要．近几年来，关于数列的应用题也常出现.
1、现有流量均为300m3/s的两条河流A、B汇合于某处后，不断混合，它们的含沙量分别为2kg/m3和0.2kg/m3．假设从汇合处开始，沿岸设有若干观测点，两股水流在流经相邻两个观测点的过程中，其混合效果相当于两股水流在1秒钟内交换100m3的水量，即从A股流入B股100m3水，经混合后，又从B股流入A股100m3水并混合．问：从第几个观测点开始，两股河水的含沙量之差小于0.01kg/m3（不考虑沙沉淀）．（1999·保送生试题）
本题考查等比数列的概念，不等式的解法，及应用数学知识解决实际问题的能力．
解析：
设第n个观测点A股水流含沙量为ankg/m3，B股水流含沙量为bn.
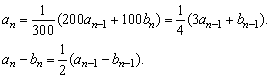
∴{an－bn}是以a1－b1为首项，
为公比的等比数列.
因此，从第9个观测点开始，两股水流含沙量之差小于0.01kg/m3.
2、（上海市高考题）设数列{an}的首项a1=1，前n项和Sn满足关系式：3tSn－(2t＋3)Sn－1=3t(t>0,n=2,3,4,…)
（1）求证：数列{an}是等比数列；
（2）设数列{an}的公比为f(t)，作数列{bn}，使b1=1,bn=f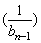
(n=2,3,4，…)，求bn.
本题考查等差数列、等比数列的概念和求和公式，以及考查逻辑推理能力与分析问题、解决问题的能力.
解：（1）由S1=a1=1,S2=a1＋a2=1＋a2，得
3t(1＋a2)－(2t＋3)=3t,
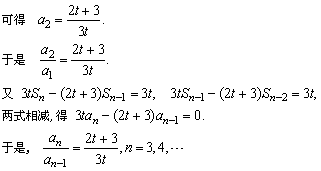
因此，{an}是一首项为1，公比为
的等比数列.
（2）
可见，{bn}是一个首项为1，公差为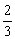
的等差数列.
于是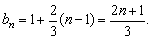
（3）由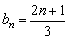 
，可得{b2n－1}和{b2n}是首项分别为1和
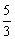，公差均为
的等差数列.
于是
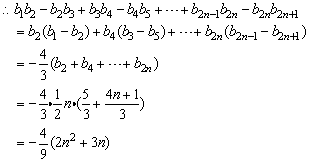
说明：
本题已知关于Sn的递推式3tSn－(2t＋3)Sn－1=3t，为求an，只要将上式的n换成n－1，得3tSn－1－(3t＋3)Sn－2=3t.要由Sn的关系式得到an的关系式，只要通过关系式Sn－Sn－1=an，将前面两式相减，即可完成（1）的证明.
（2）的证明较简单．前面所给（3）的证明技巧性强，添括号转化为数列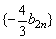
的求和．（3）还可以用下面方法求得：
