指数、指数函数作为数学运算及基本函数在高考时往往与其它知识融合在一起被考查.
1、(全国高考试题)已知c>0,设P:函数y=cx在R上单调递减;Q:不等式x+|x-2c|>1的解集为R,如果P和Q有且只有一个正确,求c的取值范围.
分析:
本题考查指数函数的性质,绝对值不等式的解,函数的最值以及命题与非命题的概念和逻辑推理能力,利用性质先分别求出满足条件
P、Q中c的取值范围,再根据命题与非命题的概念得出符合条件的c的取值范围.
解答:
函数y=cx在R上单调递减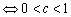 ;
;
不等式x+|x-2c|>1的解集为R 函数y=x+|x-2c|在R上恒大于1.
函数y=x+|x-2c|在R上恒大于1.
∵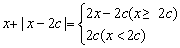
∴函数y=x+|x-2c|在R上的最小值为2c.
∴不等式x+|x-2c|>1的解集为R 2c>1,∴c>
2c>1,∴c>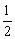 .
.
如果P正确且Q不正确,则0<c≤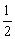 .
.
如果P不正确,且Q正确,则c≥1.
∴c的取值范围是(0,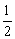 ]∪[1,+∞).
]∪[1,+∞).
2、(上海)已知函数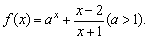
(1)证明:函数f(x)在(-1,+∞)上为增函数;
(2)用反证法证明f(x)=0没有负数根.
分析:本题考查函数的单调性和反证法.
解答:
(1)设-1<x1<x2,
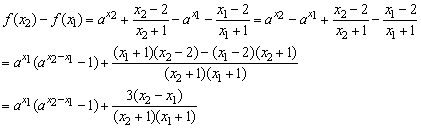
因为x2-x1>0,又a>1,所以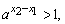 而-1<x1<x2,
而-1<x1<x2,
所以x1+1>0,x2+1>0,所以f(x2)-f(x1)>0.
∴f(x)在(-1,+∞)上为增函数
(2)设x0为方程f(x)=0的负根,则有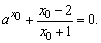

显然x0≠-1
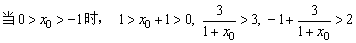
而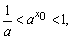 这是不可能的,即不存在0>x0>-1的解
这是不可能的,即不存在0>x0>-1的解

而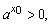 矛盾,即不存在x0<-1的解.
矛盾,即不存在x0<-1的解.
综上,即不存在负根.
3、(上海)函数f(x)=ax(a>0且a≠1)在区间[1,2]上的最大值比最小值大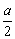 ,则a的值为________.
,则a的值为________.
解析:本题考查学生分类讨论的能力和指数函数的性质及运算能力.
解答:
a>1时,
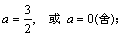
0<a<1时,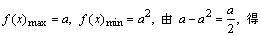

故a的值为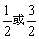 .
.