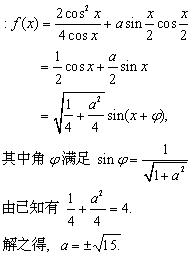正弦函数、余弦函数的图象性质是三角函数这一章中的重点，也是高考必考内容之一，这部分题目的分值约占5%，主要考查基础知识，涉及三角函数的周期性、奇偶性、单调性、最大值和最小值问题．

例1、（全国）函数y=－x·cosx的部分图像是（　）

解答：

　　函数y=－xcosx是奇函数，图像不可能是A和C，又当x∈(0，)时，y<0，所以B错，D是正确答案．

答案：D

例2、（北京）已知函数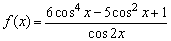，求f(x)的定义域，判断它的奇偶性，并求其值域.

分析：

　　求定义域需注意分母不能为0.判断奇偶性前注意定义域是否关于原点对称，求值域时需先对f(x)化简.

解答：

　　由cos2x≠0得

　　∴定义域是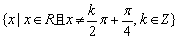

　　因f(x)的定义域关于原点对称且

　　

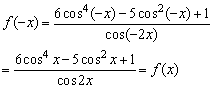
　　故f(x)是偶函数.

　　

　　所以f(x)的值域为

说明：本题注重考查倍角公式以及最小正周期的计算公式．

例3、（重庆）若函数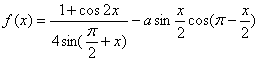的最大值为2，试确定常数a的值．

分析：

　　先将函数式化简转化为单一的三角函数，由最大值得方程解之。

解：

　　

-END-