自1998年高考考纲调整后，不要求用动量定理公式计算，降低了难度。但对动量定理的理解以及应用动量进行定性分析和半定量计算的要求没有降低。因为掌握用动量定理公式计算相关问题基本方法，有助于对相应问题作定性分析。所以“不要求用动量定理公式计算”实际是指：不要求用动量定理公式去计算人为编制的复杂问题。所以在学习中应加深对动量定理内容的理解，并掌握用动量定理公式计算的基本方法。
例1、质量为M的金属块和质量为m的木块通过细线连在一起，从静止开始以加速度a在水中下沉，经过时间t，细线断了，金属块和木块分离。再经t′，木块停止下沉，求此时金属块的速度。
解析：
对金属块和木块组成的系统，其所受的合外力为F合=(M＋m)a，从开始下沉到木块停止下沉，系统所受的合外力是恒定的。选开始的状态作为初态，木块停止下沉的状态作为末态，对全过程应用的动量定量有：
说明：
动量定理的研究对象一般为单一的物体，但也可以是一个物体系，且动量定理可以在某一分过程中使用，也可以对全过程使用。
例2、长1.8m的细绳悬挂着质量为2kg的小球，绳的另一端系在离地高3.6m的天花板上。现将小球从贴着天花板开始自由下落，在细绳被拉直的瞬间绳断裂，接着小球竖直下落到地面上，全过程历时1.2s。已知小球刚着地时的速度大小为6.5m/s，不计空气阻力，取g=10m/s2。求：
（1）细绳刚断裂时小球的速度。
（2）在细绳被拉断瞬间，绳子受到的平均拉力。
解析：
（1）设细绳断开时小球的速度为v1，着地时的速度为v2。绳断开后，小球作竖直下抛运动，运动距离h=1.8m，由匀加速运动的公式有：
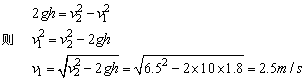
即细绳刚断开时小球的速度大小为2.5m/s，方向向下。
（2）、绳断之前，小球自由下落的时间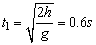
；绳断开后，小球的运动时间
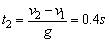，则细绳断裂所经历的时间为△t=t－t1－t2=0.2s.
细绳断裂瞬间，小球受到竖直向上的绳的拉力和竖直向下的重力，绳拉紧前小球的速度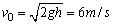
，向下；绳断裂时，小球的速度v1=2.5m/s，向下。以向下为正方向，由动量定理有：
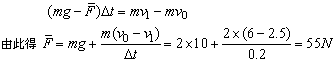
即绳断裂过程中受到平均拉力为55N.
说明：
动量定理是一个与具体物理过程有关的物理规律，涉及到力的冲量及研究对象的初、末态动量。因此，除了对研究对象进行受力分析以外，还必须分析物理过程，在建立物理图象的基础上确定初、末态。
例3、高压水枪竖直向上喷射出水柱，将一个质量为m的开口向下的铁盒顶在空中，如图所示，已知水以恒定的速度v0从横截面积为S的水枪中持续不断的喷出，冲击铁盒后速度为零，求铁盒稳定悬浮的位置距水枪口的高度。
精析：
水喷出后作竖直上抛运动，由运动学知识先求出上升h高时的速率v，以水枪在时间△t内喷出质量△m的水为研究对象，由动量定理求解即可。
解：
在△m与铁盒作用的过程中，受铁盒的作用力为F，
取竖直向下为正方向，由动量定理有：
(F＋△mg)△t=0－(－△mv)
由运动学知识知：
当△t取得极短时，△mg很小，可以忽略：
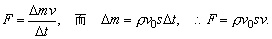
又铁盒静止，由牛顿第三定律和物体的平衡知识有：F=mg
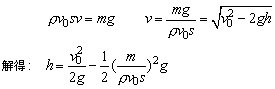
题后语：本题代表了一类问题，如水滴一滴滴落到盘子上，求盘子上受到的作用力的大小，子弹连续不断从枪中射出，求肩膀对枪托的作用力，等等。
