答案:L=0.3m
解析:
设A、C之间的滑动摩擦力大小为f1,A与水平地面之间的滑动摩擦力大小为f2
∵μ1=0.22,μ2=0.10
∴F=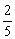 mg<f1=μ1×2mg
mg<f1=μ1×2mg
且F=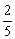 mg>f2=μ2(2m+m)g
mg>f2=μ2(2m+m)g
∴一开始A和C保持相对静止,在F的作用下向右加速运动,有
(F-f2)·s=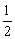 ·(2m+m)v12
·(2m+m)v12
A、B两木板的碰撞瞬间,内力的冲量远大于外力的冲量,由动量守恒定律得
Mv1=(m+m)v2
碰撞结束后到三个物体达到共同速度的相互作用过程中,设木板向前移动的位移为s1.选三个物体构成的整体为研究对象,外力之和为零,则
2mv1+(m+m)v2=(2m+m+m)v3
设A、B系统与水平地面之问的滑动摩擦力大小为f3,对A、B系统,由动能定理
f1·s1-f3·s1=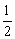 ·2mv32-
·2mv32-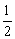 ·2mv22
·2mv22
f3=μ2(2m+m+m)g
对C物体,由动能定理F·(21+s1)-f1·(21+s1)=  ×2mv32-
×2mv32-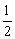 ×2mv12
×2mv12
由以上各式,再代入数据可得l=03m.
2、如图,质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向.现在挂钩上挂一质量为m3的物质C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将C换成另一个质量为(m1+m3)的物体D,仍从上述初始位置由静止状态释放,则这次B刚离地时D的速度的大小是多少?已知重力加速度g.
答案: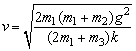
解析:
开始时,A、B静止,设弹簧压缩量为x2,有
kx1=m1g ①
挂C并释放后,C向下运动,A向上运动,设B刚要离地时弹簧伸长量为x2,有
kx2=m2g ②
B不再上升,表示此时A和C的速度为零;C已降到其最低点.由机械能守恒,与初始状态相比,弹簧弹性势能的增加量为
△E=m3g(x1+x2)-m1g(x1+x2) ③
C换成D后,当B刚离地时弹簧势能的增量与前一次相同,由能量关系得
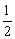 (m3+m1)v2+
(m3+m1)v2+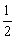 m1v2=(m3+m1)g(x1+x2)-m1g(x1+x2)-△E ④
m1v2=(m3+m1)g(x1+x2)-m1g(x1+x2)-△E ④
由③④式得
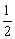 (2m1+m3)v2= m1g(x1+x2) ⑤
(2m1+m3)v2= m1g(x1+x2) ⑤
由①②⑤式得
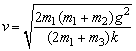 ⑥
⑥