讲解:
设物体的质量为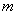 ,物体与路面之间的动摩擦因数为
,物体与路面之间的动摩擦因数为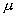 ,斜面的倾角为
,斜面的倾角为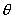 ,当物体沿DBA滑动时,由动能定理有:
,当物体沿DBA滑动时,由动能定理有: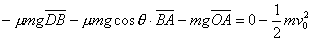 ,
,
解得:
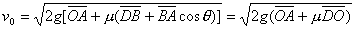 。
。
由于所得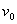 的表达式与
的表达式与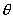 无关,故当物体沿DCA滑动时初速度也等于
无关,故当物体沿DCA滑动时初速度也等于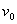 ,故正确选项为B。
,故正确选项为B。
答案:B
评析:本题涉及物体沿粗糙水平面和斜面的两段运动,涉及滑动摩擦定律,求解时需要假设一些物理量,通过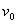 的表达式与斜面倾角
的表达式与斜面倾角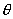 无关得出正确结论,而
无关得出正确结论,而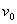 表达式的推导,可用动能定理,也可用牛顿运动定律和运动学公式,试题对学生的推理能力和分析综合能力有较高要求。
表达式的推导,可用动能定理,也可用牛顿运动定律和运动学公式,试题对学生的推理能力和分析综合能力有较高要求。
例2、质量为M的小船以速度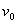 行驶,船上有两个质量皆为
行驶,船上有两个质量皆为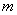 的小孩
的小孩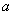 和
和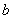 ,分别静止站在船头和船尾,现小孩
,分别静止站在船头和船尾,现小孩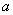 沿水平方向以速率
沿水平方向以速率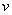 (相对于静止水面)向前跃入水中,然后小孩子
(相对于静止水面)向前跃入水中,然后小孩子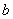 沿水平方向以同一速率(相对于静止水面)向后跃入水中,求小孩
沿水平方向以同一速率(相对于静止水面)向后跃入水中,求小孩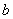 跃出后小船的速度。
跃出后小船的速度。
讲解:
整个过程中系统所受合外力为零,系统动量守恒,因两个小孩跳离船后动量的矢量和为零,故有: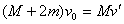 ,所以
,所以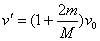 。
。
答案: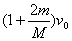
评析:本题考查动量守恒定律的应用,应用动量守恒定律应注意矢量性、系统性、同时性、相对性。本题中系统的选取、过程的选取是否恰当对本题的解关系很大,动量守恒定律的应用重点分析初末状态与中间过程无关,往往取整个过程来研究。
例3、在光滑水平地面上有两个相同的弹性小球A、B,质量都为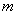 ,现B球静止,A球向B球运动,发生正碰。已知碰撞过程中总机械能守恒,两球压缩最紧时的弹性势能为
,现B球静止,A球向B球运动,发生正碰。已知碰撞过程中总机械能守恒,两球压缩最紧时的弹性势能为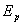 ,则碰前A球的速度等于()
,则碰前A球的速度等于()
A. 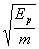 B.
B. 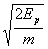
C. 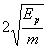 D.
D. 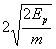
讲解:
设碰前A球的速度为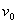 ,两球压缩最紧时的速度为
,两球压缩最紧时的速度为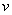 ,根据动量守恒定律得出:
,根据动量守恒定律得出:
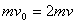 ①由能量定恒定律得:
①由能量定恒定律得: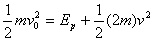 ②
②
①②两式联立求解得: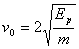 。
。
答案:C
评析:本题涉及了动量守恒定律和动能与弹性势能的转化和守恒,只要能建立能量守恒定律的方程式便可结合动量守恒联立求解。