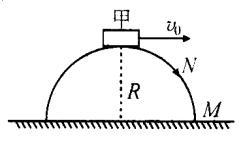
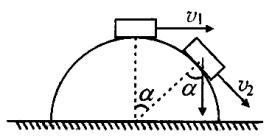
例、半径为R的光滑半圆球固定在水平面上，如图所示.顶部有一小物体甲，今给它一个水平初速度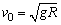
，物体甲将（ ）
A．沿球面下滑至M点
B．先沿球面下滑至某点N，然后便离开球面做斜下抛运动
C．按半径大于R的新的圆弧轨道做圆周运动
D．立即离开半圆球做平抛运动
解法一：
定性分析，物体在初始位置受竖直向下的重力，因为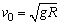
，所以，球面支持力为零，又因为物体在竖直方向向下运动，所以运动速率将逐渐增大，若假设物体能够沿球面或某一大于R的耘的圆弧做圆运动，则所需的向心力应不断增大．而重力沿半径方向的分力逐渐减少，以上两种情况又不能提供其他相应的指向圆心的力的作用，故不能提供不断增大的向心力，所以，不能维持圆运动，而立即离开半圆球做平抛运动.
解法二：
定量分析，设水平初速度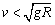
，则在最高点受重力、球面支持力，沿球面运动，设到达某点脱离球面，球面支持力减为零，如图所示，则有
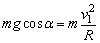①
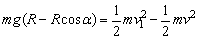②
由②得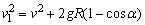
，代人①中得
gRcosα=v2＋2gR（1－cosα）.
整理得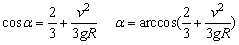
即半径R转过α角度后物体开始脱离球面.
由此可以看出α的大小取决于初速度v.
若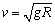
，则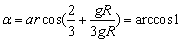
,
即α=0.立即离开半圆球做平抛运动.
答案：D
