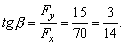将一个力分解在两个互相垂直的方向上的分解方法叫正交分解法,这种方法是物理学中用得比较普遍的一种方法,例如将一个与x轴成α夹角的力F分别到x轴和与x轴垂直的y轴上,可得:
Fx=Fcosα,
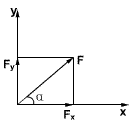
Fy=Fsinα
对几个共点力的合成也可用力的正交分解法,它是先将若干力分解到互相垂直的两个方向上,将矢量运算转化为同一直线上的代数运算,其具体作法是:
①将力向选定的互相垂直的两个坐标轴x轴和y轴方向进行分解;
②分别对x轴和y轴上的分力进行代数运算,得出合力Fx、Fy.
③再求Fx、Fy的合力,得到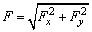 .
.
用正交分解法的好处是可以将较复杂的数学运算化为较简单的解直角三角形的问题。
例题、如图所示,为把斜面上一小车从斜面底移到斜面顶,一人在前面通过绳拉车,绳与斜面的夹角α=30°,拉力F1=40N,另一人从后面推车,推力F2=50N,推力的方向与斜面的夹角为θ=45°,求F1与F2的合力的大小和方向。
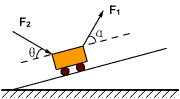
解答:沿斜面和垂直斜面方向建立xOy坐标系如图所示。

则:
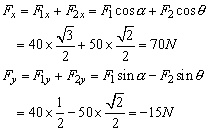
合力大小
F与x轴的夹角为β: