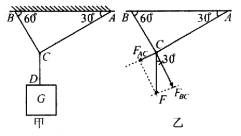
1、如图甲所示，轻绳AC与水平面夹角α=30°，BC与水平面夹角β=60°，若AC、BC能承受的最大拉力不能超过100N，那么重物G不能超过多少（设悬挂重物G的绳CD强度足够）？
解析：
此类问题的研究对象只能选结点C，因为C点能将受到的AC、BC的拉力与重物G联系起来，由于C点只受三个力且合力为零，所以最简单的求解方法就是力的合成或分解.
由于重物静止时对C点的拉力F=G，拉力产生两个效果对BC的拉力FBC和对AC的拉力FAC，其力的矢量关系如图乙，从图中关系可以看出FBC>FAC，即当重力G增加时，FBC先达到100 N.因此重力G的极限值就等于FBC=100N时所对应的F的数值，由几何关系得
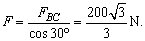
2、如图所示，物体a，b和c叠放在水平桌面上，水平力Fb=5N、Fc=10N分别作用于物体b、c上，a、b和c仍保持静止。以f1、f2、f3分别表示a与b、b与c、c与桌面间的静摩擦力的大小，则（ ）
A．f1=5N，f2=0，f3=5N B．f1=5N，f2=5N，f3=0
C．f1=0，f2=5N，f3=5N D．f1=0，f2=10N，f3=5N
解析：b受c向右静摩擦力f2与Fb平衡，c受向左f2＋f3=10N与Fc平衡.故C正确。
答案：C
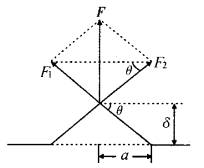
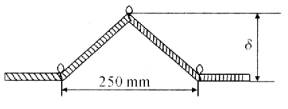
3、有些人，像电梯修理员、牵引专家和赛艇运动员，常需要知道绳或金属线中的张力，可又不能到那些绳、线的自由端去测量，一家英国公司现在制造出一种夹在绳上的仪表.用一个杠杆使绳子的某点有一个微小偏移量，如图所示.仪表很容易测出垂直于绳的回复力，推导一个能计算绳中张力的公式.如果偏移量为12mm，回复力为300 N，计算绳中张力.
解析：
设绳中张力为FT，仪器对绳的拉力F可分解为拉绳的两个力F1、F2，而F1=F2=FT，如图所示，由F1、F2、F 构成一个菱形，依图中几何关系有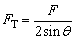
，又因微小形变，所以sinθ≈tanθ，故
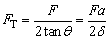.当F =300N，δ=12mm时，FT=1562.5N.
