若研究的对象包括几个相互作用的物体，它们的质量分别是m1，m2，…，mn，受到多个外力F1、F2、F3、……作用，则：F1＋F2＋F3＋……=m1a1＋m2a2＋m3a3＋……，这就是关于系统运用牛顿第二定律得到的结论，应用到解题中去有时会使问题变得简便。

例、如图所示，质量M=10kg的木楔ABC静止于粗糙的水平地面上，木楔的倾角θ=30°。斜面上有一个质量m=1.0kg的物块由静止开始沿斜面下滑，当滑行路程s=1.4m时，其速度v=1.4m/s。在此过程中木楔没有动。求地面对木楔的摩擦力的大小和方向。（取g=10m/s2）

解析：方法（1）

物块沿斜面下滑的加速度由已知条件可以直接求得

物体在斜面上运动时受重力mg、支持力N1和滑动摩擦力f1作用，受力如图（a）所示，它的运动方程为

.

将a=0.7m/s2代入，可得：

f1=mgsinθ－ma=4.3N

N1=mgcosθ=8.7N.

木楔受5个力作用而处于平衡状态之中：重力Mg、物块对它的压力N1、物块对它的滑动摩擦力f1、水平地面对它的支持力N2，水平地面对它的静摩擦力（f2方向向左）。受力如图（b），运动方程（即平衡方程）为：

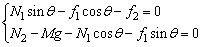
将N1=8.7N、f1=4.3N、θ=30°、M=10kg代入，求得

f2=8.7×0.5－4.3×0.87=0.61N

N2=10×10＋8.7×0.87＋4.3×0.5=109.7N.

可见，地面作用于木楔、沿水平方向向左的静摩擦力大小为0.61N。

方法（2）

由题意，根据运动学公式可求得物块的加速度a.

.

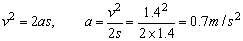对M与m组成的整体进行受力分析如图（a）所示.

把物体加速度a分解到水平方向和竖直方向上，如图（b）所示.

对m、M组成的系统应用牛顿第二定律，有：

解得f=0.61N.

-END-