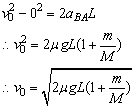长为L，质量为M的木板A静止在光滑的水平桌面上，有一质量为m的小木块B以水平速度v0恰好落在木板A的左端，如图。木块B与木板A间的摩擦系数为μ，木板B可视为质点，求：

（1）A和B的加速度各是多少？方向如何？

（2）当B运动到A长度的中点时，相对于A的速度是多少？

（3）如果最后B恰好到达A的右端不落下来，则v0的值应是多大？

解：

　　当B在A上向右运动时，B受到向左的摩擦力而被减速，这时摩擦力对B是阻力。同时A受到等量向右的摩擦力而使A加速，这时摩擦力对A是动力。在整个过程中B的速度不断减小，A 的速度不断增大，当这两个速度相等时，A和B就保持相对静止。

　　（1）以B为研究对象，如图，B受到重力mg，支持力NB和向左的摩擦力f，由牛顿第二定律得：mgμ=maB.

　　　　 ∴ aB=gμ，方向向左。

　　再以A为研究对象，如图A受到重力Mg，B对它向下的压力NB′，桌面对它的支持力NA和水平向右的摩擦力f′，由牛顿第二定律得：

　　mgμ=MaA.

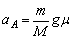　　∴ ，方向向右。

　　（2）B相对于A的加速度为aBA，如图所示，则有，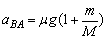

　　根据运动学公式可得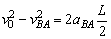

　　∴

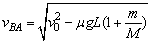
　　（3）如果要使B恰好到达A的右端不至落下，则必须B到达A的右端时的速度，恰好等于A这时的速度，也就是B和A的相对速度为零，即A、B相对静止。则有：

　　

-END-